Các câu hỏi tương tự
Phần I: Trắc nghiệmCho hình lăng trụ ABC.ABC, M là trung điểm của BB’. Đặt
C
A
→
a
→
,
C
B
→
b
→
,
A
A
→
c
→
. Khẳng định nào sau đây đúng? A.
A...
Đọc tiếp
Phần I: Trắc nghiệm
Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB’. Đặt C A → = a → , C B → = b → , A ' A → = c → . Khẳng định nào sau đây đúng?
A. A M → = b → + c → - 1 2 a →
B. A M → = a → - c → + 1 2 b →
C. A M → = a → + c → - 1 2 b →
D. A M → = b → - a → + 1 2 c →
Phần I: Trắc nghiệmCho hình chóp S.ABCD có đáy ABCD là hình bình hành. - Đặt
S
A
→
a
→
,
S
B
→
b
→
,
S
C
→
c
→
,
S
D
→
d...
Đọc tiếp
Phần I: Trắc nghiệm
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
- Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → .Khẳng định nào sau đây đúng?
A. a → + c → = d → + b →
B. a → + b → = d → + c →
C. a → + d → = b → + c →
D. a → + b → + c → + d → = 0 →
Phần I: Trắc nghiệm
Cho hàm số y = x 2 + 2 x + 2000 có đồ thị (C) . Khi đó tiếp tuyến của (C) tại điểm M( 1; 2003) có hệ số góc là:
A. k = 4
B. k = -2
C. k = 2
D. k = -4
Bài 2. (1 điểm) Trong hình sau, khi được kéo ra khơi vị trí cân bằng ờ điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$.
Tọa độ $s$ cm của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s10 sin left(10 t+dfrac{pi}{2}right)$. Vào các thời điểm nào thì $s-5 sqrt{3} $ cm?
Đọc tiếp
Bài 2. (1 điểm) Trong hình sau, khi được kéo ra khơi vị trí cân bằng ờ điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$.
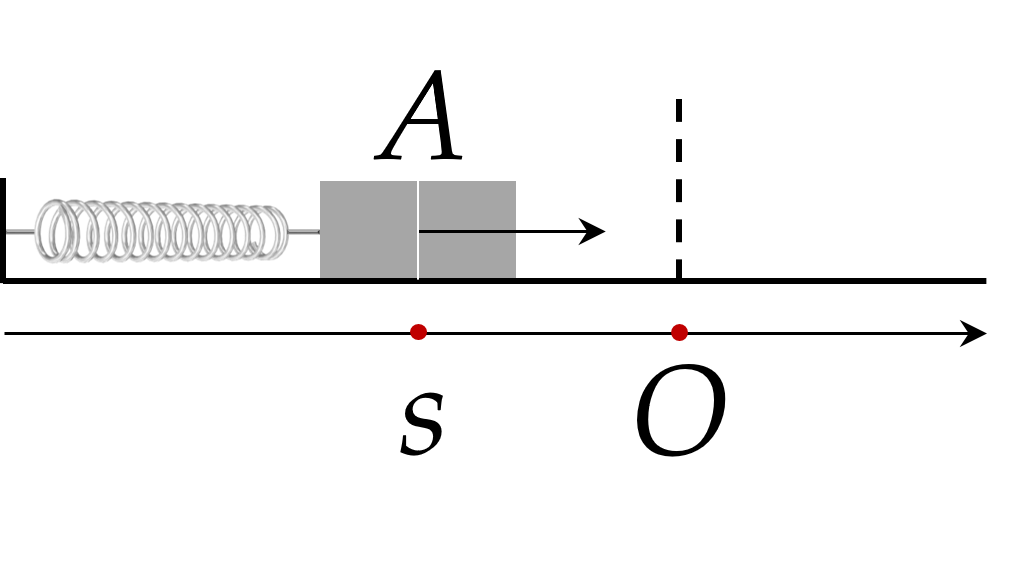
Tọa độ $s$ cm của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s=10 \sin \left(10 t+\dfrac{\pi}{2}\right)$. Vào các thời điểm nào thì $s=-5 \sqrt{3} $ cm?
Cho tam giác ABC, điểm I thoả mãn:
5
M
A
→
2
M
B
→
. Nếu
I
A
→
m
I
M
→
+
n...
Đọc tiếp
Cho tam giác ABC, điểm I thoả mãn: 5 M A → = 2 M B → . Nếu I A → = m I M → + n I B → thì cặp số (m; n) bằng:
A. 
B. 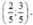
C. 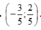
D. 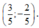
Cho M(2;–5); N(–3; 2), I(2;5). Đ I : M -> M’; Đ I : N -> N’. Tính tọa độ M ' N ' →
A. (5;7)
B. (7;5)
C.(5; –7)
D. (–7; 5)
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\sqrt{n^2-1}+3n\)
2) tính giới hạn I = \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+5}+n\right)\)
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2, 3, 3, 2 (đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng?









