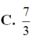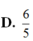ý tưởng giải nhanh câu này khá đơn giản (tính trâu bò đặt ẩn thì nó mất rất nhiều thời gian), đó là hãy tìm đường thẳng song song với \(3x+y-9=0\) và tiếp xúc với (C). Khi đó tiếp điểm chính là 2 điểm M, N cần tìm.
\(3x+y-9=0\Leftrightarrow y=-3x+9\)
Gọi tiếp điểm có hoành độ x \(\Rightarrow y'\left(x\right)=-3\)
\(\Rightarrow1-\dfrac{4}{\left(x-1\right)^2}=-3\)
\(\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=2\Rightarrow y=11\end{matrix}\right.\)
\(\Rightarrow a+b+c+d=1+1+2+11=14\)
23d.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{1}{f\left(x\right)+2}=\dfrac{1}{-\infty+2}=0\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{1}{f\left(x\right)+2}=\dfrac{1}{6+2}=\dfrac{1}{8}\)
Nên hàm có 2 TCN
24d.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{1}{2f\left(x\right)+6}=\dfrac{1}{2.\left(+\infty\right)+6}=0\Rightarrow y=0\) là TCN
\(\lim\limits_{x\rightarrow+\infty}\dfrac{1}{2f\left(x\right)+6}=\dfrac{1}{2.10+6}=\dfrac{1}{26}\Rightarrow y=\dfrac{1}{26}\) là 1 TCN
Từ BBT ta thấy đường thẳng \(y=-3\) cắt \(f\left(x\right)\) tại 1 điểm \(x=a>2\) ở nhánh bên phải của đồ thị
\(\lim\limits_{x\rightarrow-2}\dfrac{1}{2f\left(x\right)+6}=\dfrac{1}{2.\left(-3\right)+6}=\infty\Rightarrow x=-2\) là 1 TCĐ
\(\lim\limits_{x\rightarrow a}\dfrac{1}{2f\left(x\right)+6}=\lim\limits_{x\rightarrow a}\dfrac{1}{2\left[f\left(x\right)+3\right]}=\dfrac{1}{2.0}=\infty\Rightarrow x=a\) là 1 TCĐ
Vậy ĐTHS có 4 tiệm cận đứng và ngang, 2 đứng 2 ngang