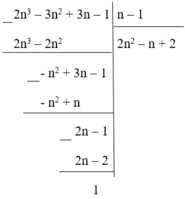
2 n 3 – 3 n 2 + 3n – 1 = (2 n 2 – n + 2)(n – 1) + 1
Để 2 n 3 – 3 n 2 + 3n – 1 chia hết cho n – 1 thì 1 chia hết cho n – 1
=> (n – 1) Є {1;-1}
n – 1 1 -1
n 2 0
P 9 1
TM TM
Vậy n Є {0; 2} để P Є Z
Đáp án cần chọn là: A

2 n 3 – 3 n 2 + 3n – 1 = (2 n 2 – n + 2)(n – 1) + 1
Để 2 n 3 – 3 n 2 + 3n – 1 chia hết cho n – 1 thì 1 chia hết cho n – 1
=> (n – 1) Є {1;-1}
n – 1 1 -1
n 2 0
P 9 1
TM TM
Vậy n Є {0; 2} để P Є Z
Đáp án cần chọn là: A
Cho M = ( x 4 y n + 1 − 1 2 x 3 y n + 2 ) : ( 1 2 x 3 y n ) − 20 x 4 y : 5 x 2 y (n Є N, x;y ≠ 0)
Chọn câu đúng
A. Giá trị của M luôn là số âm
B. Giá trị của M luôn là số dương
C. Giá trị của M luôn bằng 0
D. Giá trị của M luôn bằng 1
Cho P = 10 x x 2 + 3 x − 4 − 2 x − 3 x + 4 + x + 1 1 − x . Tìm x Є Z để P + 1 Є Z
A. x Є {-23; -5; -3; 15}
B. x Є {-23; -5; -3}
C. x Є {5; -5; -3; 15}
D. x Є {-23; 15}
Cho B = x − 1 x − 2 . Số giá trị của x Є Z để B Є Z là:
A. 3
B. 0
C. 2
D. -2
Nếu tam giác ABC có MN // BC (với M Є AB, N Є AC) thì
A. ΔAMN đồng dạng với ΔACB
B. ΔABC đồng dạng với MNA
C. ΔAMN đồng dạng với ΔABC
D. ΔABC đồng dạng với ΔANM
Cho A = 2019 n + 1 – 2019 n . Khi đó A chia hết cho số nào dưới đây với mọi n Є N.
A. 2020
B. 2018
C. 2017
D. 2016
Cho 4 x n + 2 – 8 x n (n Є N*). Khi đặt nhân tử chung x n ra ngoài thì nhân tử còn lại là
A. 4 x 2 – 2
B. 4 x 2 – 8
C. x 2 – 4
D. x 2 – 2
Cho 56 x 2 – 45y – 40xy + 63x = 7 x - 5 y m x + n với m, n Є R. Tìm m và n
A. m = 8; n = 9
B. m = 9; n = 8
C. m = -8; n = 9
D. m = 8; n = -9
Cho a x 2 – 5 x 2 – ax + 5x + a – 5 = a + m x 2 – x + n với với m, n Є R. Tìm m và n
A. m = 5; n = -1
B. m = -5; n = -1
C. m = 5; n = 1
D. m = -5; n = 1
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BP ⊥ MN; CQ ⊥ MN (P, Q Є MN). So sánh S B P Q C v à S A B C
A. S A B C = 2 S C B P Q
B. S A B C < S C B P Q
C. S A B C > S C B P Q
D. S A B C = S C B P Q