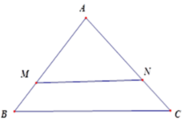
Vì MN // BC => tam giác AMN đồng dạng với tam giác ABC
Đáp án: C
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...b) Nếu
Δ
A
B
C
~
Δ
D
E
F
với tỉ số đồng dạng là 1/2 và
Δ
D
E
F
~
Δ
M
N
P
với tỉ số đồng dạng là 4/3 thì
Δ
M
N
P...
Đọc tiếp
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu Δ A B C ~ Δ D E F với tỉ số đồng dạng là 1/2 và Δ D E F ~ Δ M N P với tỉ số đồng dạng là 4/3 thì Δ M N P ~ Δ A B C với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho A I / A B = A K / B C t h ì I K / / B C . . . .
d) Hai tam giác đồng dạng thì bằng nhau....
Nếu ΔA’B’C’ = ΔABC thì tam giác A’B’C’ có đồng dạng với tam giác ABC không ? Tỉ số đồng dạng là bao nhiêu ?
Cho ΔABC vuông tại A (AB<AC), đường cao AH (H∈BC). BD là phân giác của ∠ABC (D∈AC). Gọi I là giao điểm của AH và BD.
a. Chứng minh: ΔHBA đồng dạng ΔABC và ΔHBI đồng dạng ΔABD
b. Chứng minh: \(\frac{IA}{IH}=\frac{BC}{AB}\)
c. Đường thẳng vuông góc với BD tại B cắt đường thẳng AH tại M. CHứng minh: MA.IH = MH.IA
Giúp mình ý b,c với ạ
cho ΔABC có AB=3cm; AC=4cm; BC=5cm và ΔABC đồng dạng ΔDEF với tỉ số đồng dạng là 2. vậy chu vi ΔDEF là
ΔABC 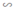ΔABC theo tỉ số đồng dạng k1, ΔABC ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác ABC đồng dạng với tam giác ABC theo tỉ số nào?
Đọc tiếp
ΔA'B'C' 
ΔA''B''C'' theo tỉ số đồng dạng k1, ΔA''B''C''
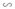ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số nào?
Cho ΔABC vuông tại A, biết AB = 3cm, AC = 4cm, phân giác (D ∈ BC)
a) Tính độ dài BC, DB, DC
b) Kẻ DK vuông góc với AC. Chứng minh ΔABC đồng dạng với ΔKDC . Tính tỉ số đồng dạng
c) Gọi I là giao điểm các đường phân giác và G là trọng tâm của ΔABC . Chứng minh rằng IG // AC.
câu cuối và cho mình xin hình
cho tam giác ABC vuông ở A , có AB=6cm, AC=8cm. vẽ đường cao AH a, tính BC b, chứng minh ΔABC đồng dạng với ΔAHB c, chứng minh AB2=BH.BC. Tính BH, HC d, vẽ phân giác AD (D ϵ BC) tính DB
Hãy chọn câu đúng. Hai ΔABC và ΔDEF có
A
^
80
∘
,
B
^
70
∘
,
F
^
30
∘
; BC 6cm. Nếu ΔABC đồng dạng với ΔDEF thì: A.
D
^
170
∘...
Đọc tiếp
Hãy chọn câu đúng. Hai ΔABC và ΔDEF có A ^ = 80 ∘ , B ^ = 70 ∘ , F ^ = 30 ∘ ; BC = 6cm. Nếu ΔABC đồng dạng với ΔDEF thì:
A. D ^ = 170 ∘ ; EF = 6cm
B. E ^ = 80 ∘ ; ED = 6cm
C. D ^ = 70 ∘
D. C ^ = 30 ∘
ΔABC đồng dạng với Δ DEF theo tỉ số đồng dạng
k
1
;ΔDEF đồng dạng với ΔGHK theo tỉ số đồng dạng
k
2
. ΔABC đồng dạng với Δ GHK theo tỉ số : A.
k
1
/
k
2
B.
k
1
+
k
2
C.
k
1
-
k
2...
Đọc tiếp
ΔABC đồng dạng với Δ DEF theo tỉ số đồng dạng k 1 ;ΔDEF đồng dạng với ΔGHK theo tỉ số đồng dạng k 2 . ΔABC đồng dạng với Δ GHK theo tỉ số :
A. k 1 / k 2
B. k 1 + k 2
C. k 1 - k 2
D. k 1 . k 2
cho ΔABC có 3 góc nhọn (ab<ac),các đường cao ak,bd,ce cắt nhau tại h.gọi m,n lần lượt là giao điểm của de với ah và bc.CMR;
a) ΔABD đồng dạng ΔACE
b) CA.CD=CB.Ck
c) ΔKDC đồng dạng ΔABc