góc B1=góc C1
=>góc ABC=góc ACB
góc KAS=góc ABC
góc SAC=góc ACB
mà góc ABC=góc ACB
nên góc KAS=góc CAS
=>AS là phân giác của góc KAC
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A có góc B = 60 độ . Tia phân giác góc B cắt AC ở D . Kẻ CK vuông góc với đường thẳng BD ở K .
a) Tính số đo góc ABD, ACB. Chứng minh tam giác BCD là tam giác cân
b) Chứng minh AB = CK
c) Chứng minh hai tam giác AKB và KAC bằng nhau
d) Chứng minh BC = 2AB
Cho tam giác ABC vuông tại A, đường trung tuyến CK
a) Cho biết BC=10cm AC=6cm. tính độ dài đoạn thẳng AB
b)trên Tia đối của tia MC lấy điểm D sao cho KD=KC. chứng minh rằng tam Giác KAC= tam giác KBD và AC = BD
c) Chứng Minh Rằng AC+BC>2CK
Cho tam giác ABC cân tại A, tia phân giác góc A cắt BC tại D.
a) Chứng minh DB = DC.
b) Kẻ DH AB (HAB), DK AC (KAC). Chứng minh DHK cân.
c) Chứng minh HK // BC. Cho tam giác ABC cân tại A, tia phân giác góc A cắt BC tại D.
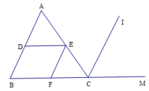
Cho hình vẽ bên, biết DE // BC ; CI là tia phân giác của ACM ^ ; EF // CI . Chứng minh rằng EF là tia phân giác của DEC ^
Cho tam giác ABC có 3 góc nhọn (AB<AC), đường cao AD và BE. Tia phân giác của góc DAC cắt BE, BC theo thứ tự ở I và K. Tia phân giác của góc EBC cắt AD, AC theo thứ tự M và N. Chứng minh tam giác MINK là hình thoi
cho tam giác abc nhọn ( ab ac ) , gọi m là trung điểm của bc . trên tia đối của tia MA, lấy điểm n sao cho ma mna) chứng minh AB // CNb) tia phân giác của góc ABC cắt tia AM tại I. Tia phân giác của góc BCN cắt tia AM tại J. Chứng Minh BICJc) Từ I vẽ tia Ix// BC ( tia Ix và điểm B nằm ở hai nửa mặt phẳng đối nhau, bờ là AM) . Trên tia Ix lấy điểm K sao cho IK BC . chứng minh rằng 3 điểm J , C , K thẳng hàng ( nếu được vẽ giúp hình luôn ạ. )
Đọc tiếp
cho tam giác abc nhọn ( ab < ac ) , gọi m là trung điểm của bc . trên tia đối của tia MA, lấy điểm n sao cho ma = mn
a) chứng minh AB // CN
b) tia phân giác của góc ABC cắt tia AM tại I. Tia phân giác của góc BCN cắt tia AM tại J. Chứng Minh BI=CJ
c) Từ I vẽ tia Ix// BC ( tia Ix và điểm B nằm ở hai nửa mặt phẳng đối nhau, bờ là AM) . Trên tia Ix lấy điểm K sao cho IK = BC . chứng minh rằng 3 điểm J , C , K thẳng hàng
( nếu được vẽ giúp hình luôn ạ. )
Cho tam giác ABC nhọn ( AB AC) . AK là tia phân giác của góc BAC ( K € BC). Gọi E, F lần lượt là hình chiếu của K trên AB, AC.a. CM : KE KF và AK là đường trung trực của đoạn thẳng EF.b. Trên tia đối của tia AB lấy điểm I sao cho AI AC. Kẻ BB vuông góc IC (H € IC). CM BIBC. Từ đó chứng minh HC HIc. Gọi S là trung điểm của IC. CM BH//AS.d. Tìm điều kiện ▲ ABC để K là trung điểm của BC
Đọc tiếp
Cho tam giác ABC nhọn ( AB< AC) . AK là tia phân giác của góc BAC ( K € BC). Gọi E, F lần lượt là hình chiếu của K trên AB, AC.
a. CM : KE= KF và AK là đường trung trực của đoạn thẳng EF.
b. Trên tia đối của tia AB lấy điểm I sao cho AI = AC. Kẻ BB vuông góc IC (H € IC). CM BI>BC. Từ đó chứng minh HC < HI
c. Gọi S là trung điểm của IC. CM BH//AS.
d. Tìm điều kiện ▲ ABC để K là trung điểm của BC
Bài 2: Cho tam giác ABC có góc a = 90độ và BC = 2AB, E là trung điểm của BC. Tia phân giác của góc B cắt cạnh AC ở D. a . Chứng minh DB là tia phân giác của góc ADE; b . Chứng minh BD = DC ; c . Tính góc B và góc C của tam giác ABC.
cho tam giác abc có 3 góc nhọn và O là trung điểm cạnh BC. Trên tia đối cua OA lấy điểm D sao cho OA=OD. vẽ AH vuông góc với BC tại H và DK vuông góc với BC tại K. Chứng minh tam giác AHO= tam giác DKO , góc KAC = góc HDB
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC).Tia phân giác của
H
A
B
^
cắt BC ở D.a) Chứng minh tam giác ACD là tam giác cân.b) Các tia phân giác của
H
A
C
^
và
A
H
C
^
cắt nhau ở I. Chứng minh. CI...
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC).
Tia phân giác của H A B ^ cắt BC ở D.
a) Chứng minh tam giác ACD là tam giác cân.
b) Các tia phân giác của H A C ^ và A H C ^ cắt nhau ở I. Chứng minh. CI đi qua trung điểm, của AD. Từ đó tính góc A I C ^ .