e: \(sin300^0=sin\left(360^0-60^0\right)=sin\left(-60^0\right)=-sin60^0=-\dfrac{\sqrt{3}}{2}\)
\(cos330^0=cos\left(360^0-30^0\right)=cos\left(-30^0\right)=\dfrac{\sqrt{3}}{2}\)
\(tan315^0=tan\left(360^0-45^0\right)=tan\left(-45^0\right)=-1\)
\(cot315=\dfrac{1}{tan315}=-1\)
c: \(sin210^0=sin\left(180^0+30^0\right)\)
\(=sin180^0\cdot cos30^0+cos180^0\cdot sin30^0\)
\(=0\cdot\dfrac{\sqrt{3}}{2}+\left(-1\right)\cdot\dfrac{1}{2}=-\dfrac{1}{2}\)
\(cos225=cos\left(180+45\right)=cos180\cdot cos45-sin180\cdot sin45\)
\(=\left(-1\right)\cdot\dfrac{\sqrt{2}}{2}-0\cdot\dfrac{\sqrt{2}}{2}=-\dfrac{\sqrt{2}}{2}\)
\(tan\left(240^0\right)=tan\left(360^0-120^0\right)=tan\left(-120^0\right)=-tan120^0=\sqrt{3}\)
\(cot\left(-\dfrac{7}{6}\Omega\right)=cot\left(-2\Omega+\dfrac{5}{6}\Omega\right)=cot\left(\dfrac{5}{6}\Omega\right)\)
\(=-\sqrt[]{3}\)
d: \(sin330^0=sin\left(360^0-30^0\right)=sin\left(-30^0\right)=-sin30^0=-\dfrac{1}{2}\)
\(cos420^0=cos\left(360^0+60^0\right)=cos60^0=\dfrac{1}{2}\)
\(tan300^0=tan\left(360^0-60^0\right)=tan\left(-60^0\right)=-\sqrt{3}\)
\(cot750^0=cot\left(720^0+30^0\right)=cot30^0=tan60^0=\sqrt{3}\)
a: \(sin150^0=sin\left(90^0+60^0\right)\)
\(=sin90^0\cdot cos60^0+cos90^0\cdot sin60^0\)
\(=1\cdot\dfrac{1}{2}+0\cdot\dfrac{\sqrt{3}}{2}=\dfrac{1}{2}\)
\(cos135=cos\left(180-45\right)\)
\(=cos180\cdot cos45+sin180\cdot sin45\)
\(=\left(-1\right)\cdot\dfrac{\sqrt{2}}{2}+0\cdot\dfrac{\sqrt{2}}{2}=-\dfrac{\sqrt{2}}{2}\)
\(tan\left(\dfrac{2}{3}\Omega\right)=tan\left(\Omega-\dfrac{1}{3}\Omega\right)=\dfrac{tan\left(\Omega\right)-tan\left(\dfrac{\Omega}{3}\right)}{1+tan\Omega\cdot tan\left(\dfrac{\Omega}{3}\right)}\)
\(=\dfrac{0-\sqrt{3}}{1+0\cdot\sqrt{3}}=-\sqrt{3}\)
\(cot\left(-\dfrac{\Omega}{4}\right)=-cot\left(\dfrac{\Omega}{4}\right)=-1\)
b: \(sin\left(\dfrac{29\Omega}{6}\right)=sin\left(4\Omega+\dfrac{5}{6}\Omega\right)=sin\left(\dfrac{5}{6}\Omega\right)\)
\(=sin\left(\Omega-\dfrac{\Omega}{6}\right)=sin\Omega\cdot cos\left(\dfrac{\Omega}{6}\right)-cos\Omega\cdot sin\left(\dfrac{\Omega}{6}\right)\)
\(=0\cdot\dfrac{\sqrt{3}}{2}-\left(-1\right)\cdot\dfrac{1}{2}=\dfrac{\sqrt{3}+1}{2}\)
\(cos\left(\dfrac{2017\Omega}{3}\right)=cos\left(672\Omega+\dfrac{\Omega}{3}\right)=cos\left(\dfrac{\Omega}{3}\right)=\dfrac{1}{2}\)
\(tan\left(-\dfrac{159\Omega}{4}\right)=-tan\left(\dfrac{159\Omega}{4}\right)=-tan\left(40\Omega-\dfrac{\Omega}{4}\right)=-tan\left(-\dfrac{\Omega}{4}\right)=tan\left(\dfrac{\Omega}{4}\right)=1\)
\(cot\left(-\dfrac{115\Omega}{6}\right)=-cot\left(\dfrac{115\Omega}{6}\right)=-cot\left(20\Omega-\dfrac{5}{6}\Omega\right)\)
\(=cot\left(\dfrac{5}{6}\Omega\right)=-\sqrt{3}\)
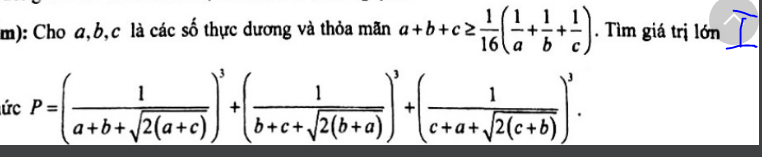mọi người giúp em với em cảm ơn nhiều lắmmmmm
