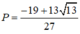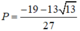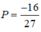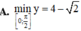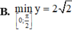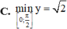\(y=cos2x-sinx+3\)
\(=1-2sin^2x-sinx+3\)
\(=-2sin^2x-sinx+4\) (1)
Vì phương trình (1) có nghiệm sinx ∈ [-1;1] nên ta có bảng biến thiên: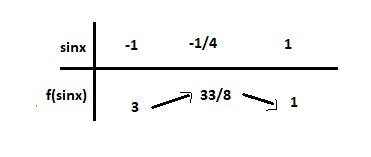
Vậy \(y_{min}=1\Leftrightarrow sinx=1\); \(y_{max}=\dfrac{33}{8}\Leftrightarrow sinx=-\dfrac{1}{4}\)
Do \(-1\le cos4x\le1\Rightarrow0\le cos^24x\le1\)
\(\Rightarrow-3\le-3cos^24x\le0\)
\(\Rightarrow2\le5-3cos^24x\le5\)
Vậy \(y_{min}=2\) khi \(cos^24x=1\)
\(y_{max}=5\) khi \(cos4x=0\)
b.
\(y=\left(1-2sin^2x\right)-sinx+3=-2sin^2x-sinx+4\)
\(y=-2\left(sinx+\dfrac{1}{4}\right)^2+\dfrac{33}{8}\le\dfrac{33}{8}\)
\(y_{max}=\dfrac{33}{8}\) khi \(sinx=-\dfrac{1}{4}\)
\(y=-2sin^2x-sinx+4=\left(-2sin^2x-sinx+3\right)+1\)
\(=\left(1-sinx\right)\left(2sinx+3\right)+1\)
Do \(-1\le sinx\le1\Rightarrow\left\{{}\begin{matrix}1-sinx\ge0\\2sinx+3>0\end{matrix}\right.\)
\(\Rightarrow\left(1-sinx\right)\left(2sinx+3\right)\ge0\)
\(\Rightarrow y\ge1\)
\(y_{min}=1\) khi \(sinx=1\)