a: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
\(\hat{ABD}=\hat{HBI}\)
Do đó: ΔBAD~ΔBHI
=>\(\frac{BA}{BH}=\frac{BD}{BI}\)
=>\(BA\cdot BI=BH\cdot BD\)
b: Xét ΔBAH có BI là phân giác
nên \(\frac{IA}{IH}=\frac{BA}{BH}\) (1)
Xét ΔBAC có BD là phân giác
nên \(\frac{BC}{BA}=\frac{DC}{DA}\) (2)
Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc HBA chung
Do đó: ΔBHA~ΔBAC
=>\(\frac{BH}{BA}=\frac{BA}{BC}\)
=>\(\frac{BA}{BH}=\frac{BC}{BA}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\frac{IA}{IH}=\frac{DC}{DA}\)
=>\(AI\cdot AD=IH\cdot DC\)
c: Ta có: ED⊥AC
AB⊥CA
Do đó: ED//AB
=>\(\hat{IAB}=\hat{IFD}\)
Xét ΔIAB và ΔIFD có
\(\hat{IAB}=\hat{IFD}\)
\(\hat{AIB}=\hat{FID}\) (hai góc đối đỉnh)
Do đó: ΔIAB~ΔIFD
=>\(\frac{IA}{FI}=\frac{AB}{FD}\)
=>\(\frac{AI}{AB}=\frac{FI}{FD}\)
=>\(AI\cdot FD=FI\cdot AB\)














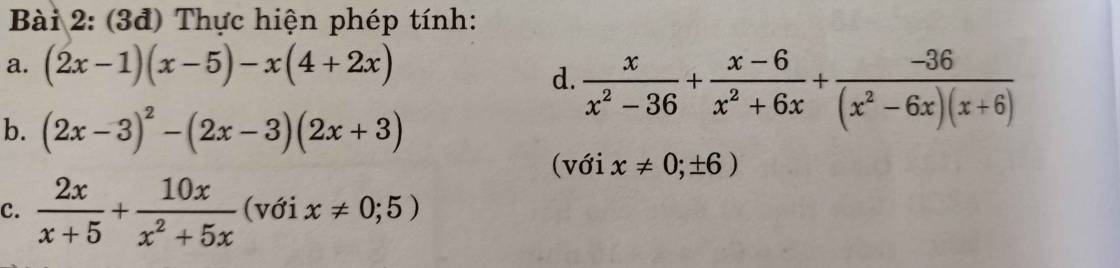


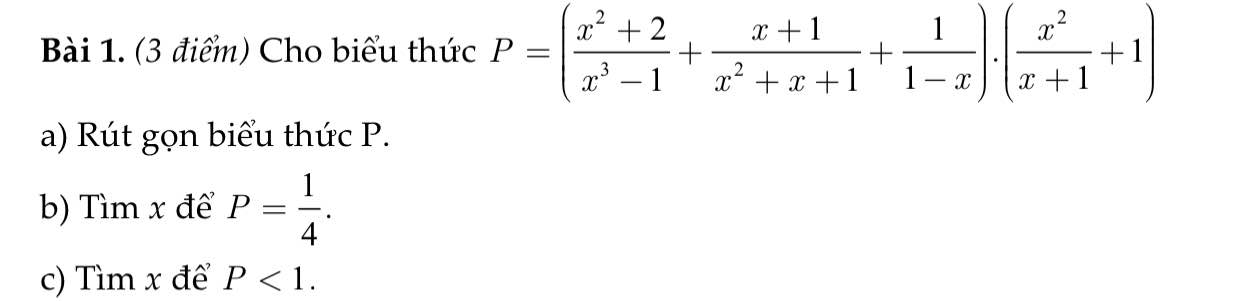

 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn





