\(=-1+\sqrt{2}-\sqrt{2}+\sqrt{3}-....-\sqrt{2024}+\sqrt{2025}\)
\(=\sqrt{2025}-1\)
`1)`\(S=\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{2024}+\sqrt{2025}}\)
\(S=\dfrac{1-\sqrt{2}}{-1}+\dfrac{\sqrt{2}-\sqrt{3}}{-1}+...+\dfrac{\sqrt{2024}-\sqrt{2025}}{-1}\)
\(S=\dfrac{1-\sqrt{2}+\sqrt{2}-\sqrt{3}+...+\sqrt{2024}-\sqrt{2025}}{-1}\)
\(S=\dfrac{1-\sqrt{2025}}{-1}\)
\(S=\sqrt{2025}-1\)
`2)`\(x=\dfrac{1}{3}\left(\sqrt[3]{\dfrac{23+\sqrt{513}}{4}}+\sqrt[3]{\dfrac{23-\sqrt{513}}{4}}-1\right)\)
\(\Leftrightarrow3x=\sqrt[3]{\dfrac{23+\sqrt{513}}{4}}+\sqrt[3]{\dfrac{23-\sqrt{513}}{4}}-1\)
\(\Leftrightarrow\left(3x+1\right)^3=\left(\sqrt[3]{\dfrac{23+\sqrt{513}}{4}}+\sqrt[3]{\dfrac{23-\sqrt{513}}{4}}\right)^3\)
\(\Leftrightarrow\left(3x+1\right)^3=\dfrac{23+\sqrt{513}}{4}+\dfrac{23-\sqrt{513}}{4}+3\sqrt[3]{\dfrac{\left(23+\sqrt{513}\right)\left(23-\sqrt{513}\right)}{4.4}}\left(\sqrt[3]{\dfrac{23+\sqrt{513}}{4}}+\sqrt[3]{\dfrac{23-\sqrt{513}}{4}}\right)\)
\(\Leftrightarrow\left(3x+1\right)^3=\dfrac{23+\sqrt{513}+23-\sqrt{513}}{4}+3\sqrt[3]{\dfrac{23^2-513}{16}}\left(3x+1\right)\)
\(\Leftrightarrow\left(3x+1\right)^3=\dfrac{23}{2}+3.\left(3x+1\right)\)
\(\Leftrightarrow\left(3x+1\right)^3=\dfrac{29}{2}+9x\)
\(\Leftrightarrow27x^3+27x^2+9x+1=\dfrac{29}{2}+9x\)
\(\Leftrightarrow27x^3+27x^2-\dfrac{27}{2}=0\)
\(\Leftrightarrow x^3+x^2-\dfrac{1}{2}=0\)
\(\Leftrightarrow2x^3+2x^2-1=0\)
\(\Leftrightarrow2x^3+2x^2=1\)
\(A=2x^3+2x^2+1\)
\(A=1+1\)
\(A=2\)
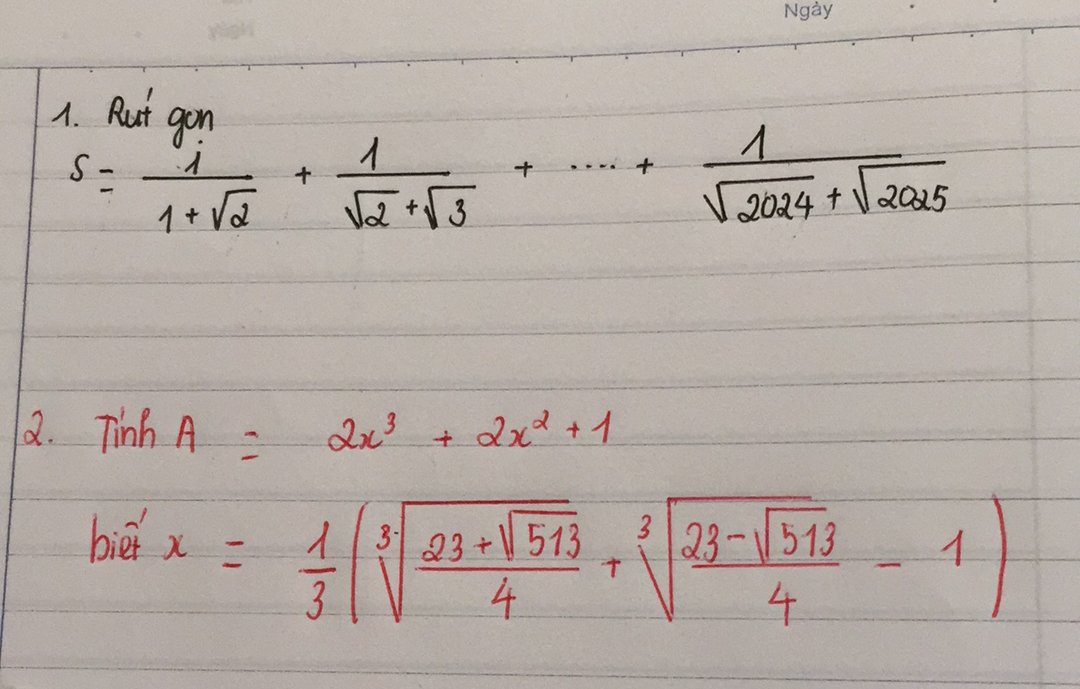
em nhờ các thầy cô gợi ý lời giải bài 17 và 18 giúp em ạ
