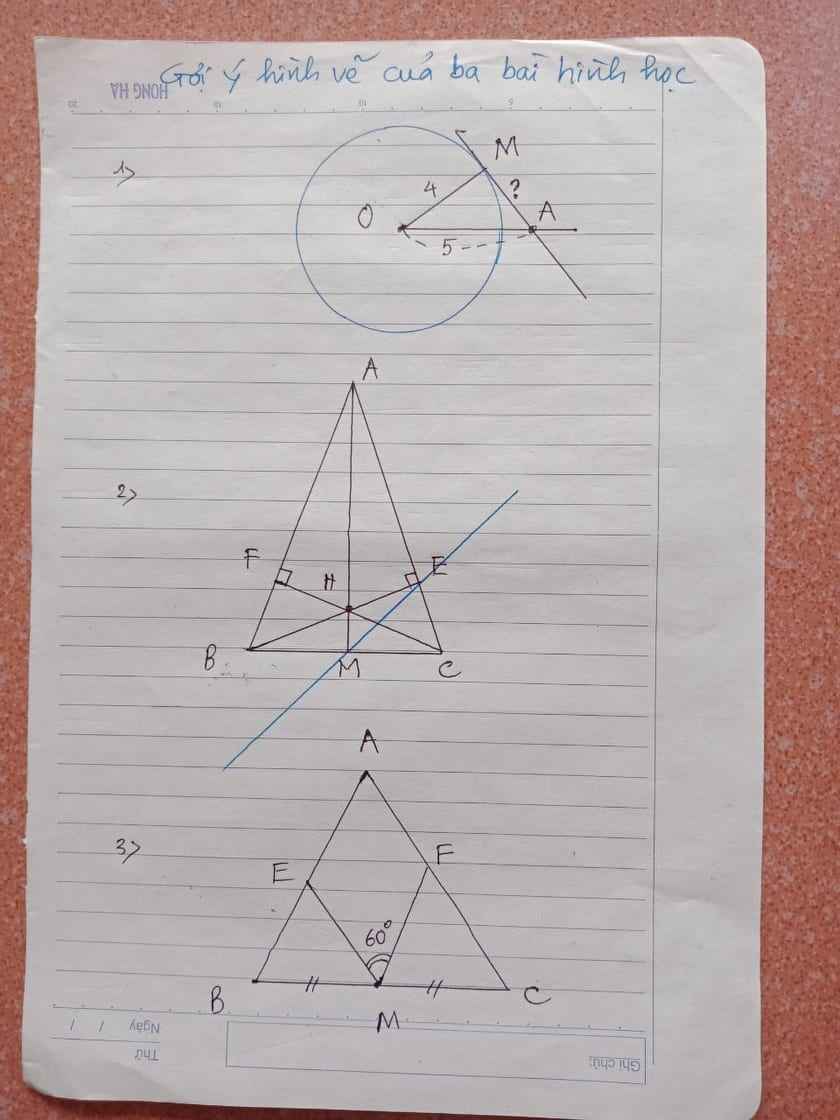
1 . Cho tam giác ABC có góc A 90o,AB 80 cm,AC60 cm,AH là đường cao, AI là phân giác(H và I thuộc BC)a.Tính BC,AH,BI,CIb.Chứng minh tam giác ABC và tam giác HAC đồng dạngc.HM và HN là phân giác của tam giác ABH và tam giác ACH. Chứng monh tam giác MAH và tam giác NCH đồng dạng.d.Chứng minh tam giác ABC và tam giác HMN đồng dạng rồi chứng minh tam giác MAN vuông câne.Phân giác của góc ACB cắt HN ở E, phân giác của góc ABC cắt HM ở F. Chứng minh EF song song với MNf.Chứng minh:BF.ECAF. AE2 , Cho ta...
Đọc tiếp
1 . Cho tam giác ABC có góc A =90o,AB =80 cm,AC=60 cm,AH là đường cao, AI là phân giác(H và I thuộc BC)
a.Tính BC,AH,BI,CI
b.Chứng minh tam giác ABC và tam giác HAC đồng dạng
c.HM và HN là phân giác của tam giác ABH và tam giác ACH. Chứng monh tam giác MAH và tam giác NCH đồng dạng.
d.Chứng minh tam giác ABC và tam giác HMN đồng dạng rồi chứng minh tam giác MAN vuông cân
e.Phân giác của góc ACB cắt HN ở E, phân giác của góc ABC cắt HM ở F. Chứng minh EF song song với MN
f.Chứng minh:BF.EC=AF. AE
2 ,
Cho tam giác ABC có 3 góc nhọn. Các đường cao lần lượt là AD , BE, CF cắt nhau tại H.
a)Chứng minh tam giác AEF đồng dạng với tam giác ABC.
b)Chứng minh tam giác AEF đồng dạng với tam giác DBF.
3 .
Cho tam giác ABC vuông tại A , AB=9cm; AC=12cm. đường cao AH, đường phân giác BD.Kẻ DE vuông góc với BC(E thuộc BC), đường thẳng DE cắt đường thẳng AB tại F.
a.Tính BC, AH?
b.Chứng minh tam giác EBF đồng dạng với tam giác EDC
c.Gọi I là giao điểm của AH và BD.Chứng minh.AB.BI=BH.BD
d.Chứng minh BD vuông góc với CF
e.Tính tỉ số diện tích của 2 tam giác ABC và BCD
giải phương trình : x^2 - 2x -3=-4