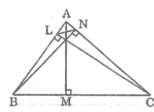
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)
Gọi AM, BN, CL là 3 đường cao của tam giác ABC(nhọn). Chứng minh:
a) Tam giác ANL đồng dạng vs tam giác ABC
b) AN .BL . CM = AB . BC . CA . CosA . CosB . CosC
Làm ơn giúp mình nha !
BÀI 1 : Gọi AM, BN, CL là ba đường cao của tam giác ABC .Chứng minh
a) tam giác ANL đồng dạng tam giác ABC
b) AN.BL.CM=AB.BC.CA.cosA.cosB.cosC
BÀI 2: Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm
a) Tính BC, góc B, góc C
b) phân giác của góc A cắt BC tại D .Tính BD,CD
Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh: AN.BL.CM = AB.BC.CA.cosA.cosB.cosC
BÀI 1 : Gọi AM, BN, CL là ba đường cao của tam giác ABC .Chứng minh
a) tam giác ANL đồng dạng tam giác ABC
b) AN.BL.CM=AB.BC.CA.cosA.cosB.cosC
BÀI 2: Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm
a) Tính BC, góc B, góc C
b) phân giác của góc A cắt BC tại D .Tính BD,CD
cho tam giác ABC vuông tại A. Kẻ đường cao AH. Gọi I,K tương ứng là tâm các đường tròn nội tiếp tam giác ABH và tam giác ACH
1/Chứng minh tam giác ABC đồng dạng với tam giác HIK
2/ Đường thẳng IK cắt AB,AC lần lượt tại M,N
a/ Chứng minh tứ giác HNCK nội tiếp trong một đường tròn
b/ Chứng minh AM=AN
C/ Chứng minh S'<=1/2S trong đó S,S' lần lượt là diện tích tam giác ABC và tam giác AMN
cho tam giác ABC vuông tại A. Kẻ đường cao AH. Gọi I,K tương ứng là tâm các đường tròn nội tiếp tam giác ABH và tam giác ACH
1/Chứng minh tam giác ABC đồng dạng với tam giác HIK
2/ Đường thẳng IK cắt AB,AC lần lượt tại M,N
a/ Chứng minh tứ giác HNCK nội tiếp trong một đường tròn
b/ Chứng minh AM=AN
C/ Chứng minh S'<=1/2S trong đó S,S' lần lượt là diện tích tam giác ABC và tam giác AMN
cho tam giác ABC vuông tại A (AB<AC). Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi S là giao điểm của AI và DE. a) Chứng minh tam giác IAB đồng dạng tam giác EAS. b)Gọi K là trung điểm AB, O là trung điểm BC. Chứng minh K, S, O thẳng hàng. c)Gọi giao điểm của KI và AC là M. Đường cao AH của tam giác ABC cắt DE tại N. Chứng minh AM=AN
cho tam giác ABC vuông tại A (AB<AC). Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi S là giao điểm của AI và DE. a) Chứng minh tam giác IAB đồng dạng tam giác EAS.
b)Gọi K là trung điểm AB, O là trung điểm BC. Chứng minh K, S, O thẳng hàng.
c)Gọi giao điểm của KI và AC là M. Đường cao AH của tam giác ABC cắt DE tại N. Chứng minh AM=AN
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Kẻ đường cao AH và đường kính AD. Gọi M và N lần lượt là hình chiếu vuông góc của B và C trên AD. Chứng minh rằng tam giác ABC đồng dạng với tam giác HMN và trung điểm I của cạnh BC cũng là tâm đường tròn ngoại tiếp tam giác HMN.
