ABN vuông tại N nên AN = AB.cosB (1)
∆ BCL vuông tại L nên BL = BC.cosB (2)
∆ ACM vuông tại M nên CM = AC.cosC (3)
Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cosA cosB cosC

ABN vuông tại N nên AN = AB.cosB (1)
∆ BCL vuông tại L nên BL = BC.cosB (2)
∆ ACM vuông tại M nên CM = AC.cosC (3)
Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cosA cosB cosC
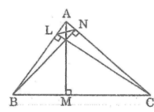
BÀI 1 : Gọi AM, BN, CL là ba đường cao của tam giác ABC .Chứng minh
a) tam giác ANL đồng dạng tam giác ABC
b) AN.BL.CM=AB.BC.CA.cosA.cosB.cosC
BÀI 2: Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm
a) Tính BC, góc B, góc C
b) phân giác của góc A cắt BC tại D .Tính BD,CD
BÀI 1 : Gọi AM, BN, CL là ba đường cao của tam giác ABC .Chứng minh
a) tam giác ANL đồng dạng tam giác ABC
b) AN.BL.CM=AB.BC.CA.cosA.cosB.cosC
BÀI 2: Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm
a) Tính BC, góc B, góc C
b) phân giác của góc A cắt BC tại D .Tính BD,CD
Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh: Tam giác ANL và tam giác ABC đồng dạng
Gọi AM ,BN,CL là ba đường cao của tam giác ABC . Chứng minh :
\(\Delta ANL\)~ \(\Delta ABC\)\(\frac{AN.BL.CM}{AB.BC.CA}\)=\(\cos A\).\(\cos B\).\(\cos C\)Gọi AM, BN, CL là 3 đường cao của tam giác ABC(nhọn). Chứng minh:
a) Tam giác ANL đồng dạng vs tam giác ABC
b) AN .BL . CM = AB . BC . CA . CosA . CosB . CosC
Làm ơn giúp mình nha !
CHo tam giác ABC có 3 =góc nhọn và H là trực tâm . Gọi M,N,P,Q lần lượt là giao điểm thứ 2 của các đường thảng AH, BH, CH với đường tròn ngoại tiếp tam giác ABC; D,E,F lần lượt là chân các đường cao hạt từ A,B,C của tam giác ABC. Chứng minh tam giác MHC cân và tính tổng \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CP}{CF}\)
Goi AM, BN, CL la ba duong cao cua tam giac ABC. Cm:
a. Tam giac ANL dong dang tam giac ABC.
b. AN.BL.CM = AB.BC.CA.cosAcosBcosC.
Mn giup mk nha cam on mn nhieu
Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chứng minh KB là tia phân giác của ∠ LKI
Cho tam giác ABC vuông tậ A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc kẻ từ H đến AB, AC. M là trung điểm của BC. a) Chứng minh EF vuông góc với AM b)Gọi S là diện tích tam giác ABC. Chứng minh 2S=AH^4/HE.HF
Làm câu b) được rồi ạ