\(\dfrac{1}{2}\cdot2^n+4\cdot2^n=9\cdot5^n\)
=>\(\dfrac{9}{2}\cdot2^n=9\cdot5^n\)
=>\(2^n=9\cdot5^n:\dfrac{9}{2}=2\cdot5^n\)
=>\(\left(\dfrac{2}{5}\right)^n=2\)
=>\(n=log_{\dfrac{2}{5}}2\)
a) \(\dfrac{1}{2}.2^n+4.2^n=9.5^n\)
\(\left(\dfrac{1}{2}+4\right).2^n=9.5^n\)
\(\dfrac{9}{2}.2^n=9.5^n\)
\(2^n=9.5^n:\dfrac{9}{2}\)
\(\left(\dfrac{2}{5}\right)^n=2\)
\(\Rightarrow\)Không có giá trị \(n\) thỏa mãn

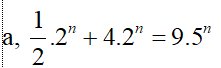 nhanh giup mik v a
nhanh giup mik v a 





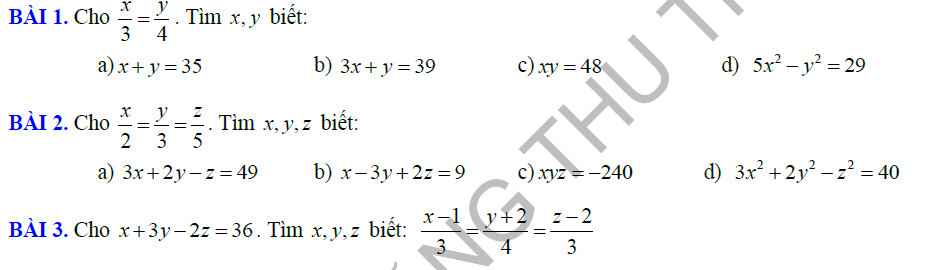









 cac ban giup mik voi a
cac ban giup mik voi a