Đặt \(t=\sin\left(x\right)\Rightarrow dt=\cos\left(x\right)\)
\(\Rightarrow\int e^{3\sin x}.\cos xdx=\int e^{3t}dt=\dfrac{1}{3}.e^{3t}+C=\dfrac{1}{3}.e^{3\sin x}+C\)
Đặt \(t=\sin\left(x\right)\Rightarrow dt=\cos\left(x\right)\)
\(\Rightarrow\int e^{3\sin x}.\cos xdx=\int e^{3t}dt=\dfrac{1}{3}.e^{3t}+C=\dfrac{1}{3}.e^{3\sin x}+C\)
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Tìm nguyên hàm của các hàm số sau ∫ ( 2 x + 3 ) e - x d x
A. - e - x ( 2 x - 1 ) + C
B. - e - x ( 2 x + 1 ) + C
C. - e x ( 2 x - 1 ) + C
D. Đáp án khác
Tính các nguyên hàm sau: ∫ e x e x + e - x d x , đặt u = e 2 x + 1
Tìm nguyên hàm sau:
\(\int\dfrac{x^4}{\left(x^4-1\right)^3}\) và \(\int\dfrac{x^8}{\left(x^4-1\right)^3}\)
Biết kết quả tích phân\(I=\)\(\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}\dfrac{\cos x}{\sin x+1}dx=aln2+bln3\) với \(a,b\) nguyên.Gía trị của \(H=a.b\) là
Gọi M và n lần lượt là gtln và gtnn của hàm số y= cos^2* x/3+ sin*x/3+1. Tính tổng M+n
Tính nguyên hàm ∫ ln ( ln x ) x d x
![]()
![]()
![]()
![]()
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 ; f ( e ) = 2 Tích phân ∫ 1 e f ' ( x ) ln x d x
A. 1
B. 0
C. 2
D. 3
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
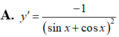
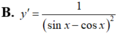
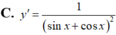

Tìm họ nguyên hàm của hàm số sau ∫ x 2 + 1 . x d x
A. 1 3 ( x 2 + 1 ) 3
B. 1 2 ( x 2 + 1 ) 3 + C
C. 1 3 ( x 2 + 1 ) 3 + C
D. 1 3 ( - x 2 + 1 ) 3 + C