Lời giải:
Dựa theo công thức $d(u(x))=u'(x)dx$ ta có:
\(\int \frac{\sin x-\cos x}{\sin x+\cos x}dx=-\int \frac{\cos x-\sin x}{\sin x+\cos x}dx=-\int \frac{d(\sin x+\cos x)}{\sin x+\cos x}\\ =-\ln |\sin x+\cos x|+C\)
Cho F x = - 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f'(x)lnx.
A. ∫ f ' x d x = ln x x 3 + 1 3 x 3 + C
B. ∫ f ' x d x = - ln x x 3 + 1 3 x 3 + C
C. ∫ f ' x d x = - ln x x 3 + 1 5 x 3 + C
D. ∫ f ' x d x = ln x x 3 + 1 5 x 3 + C
Cho biết hàm số f(x) có đạo hàm f'(x) liên tục và có một nguyên hàm là hàm số F(x). Tìm nguyên hàm
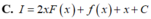
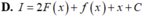
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
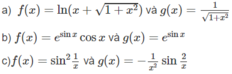
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
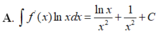
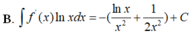
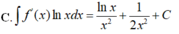
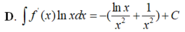
Cho F ( x ) = x 2 là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
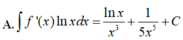
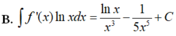
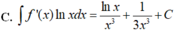
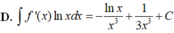
Cho F ( x ) = ( x - 1 ) e x là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
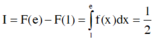
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f x = sin 2 1 x và g x = - 1 x 2 sin 2 x
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f x = e sinx cosx và g x = e sinx
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f x = ln x + 1 + x 2 và g x = 1 1 + x 2
