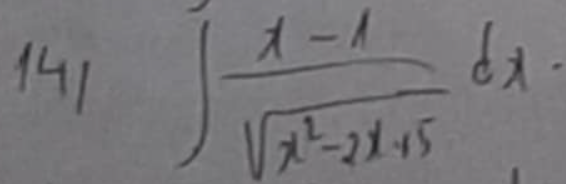Lời giải:
\(\int \frac{x-1}{\sqrt{x^2-2x+5}}dx=\frac{1}{2}\int \frac{2x-2}{\sqrt{x^2-2x+5}}dx=\frac{1}{2}\int \frac{d(x^2-2x+5)}{\sqrt{x^2-2x+5}}\\
=\frac{1}{2}\int (x^2-2x+5)^{\frac{-1}{2}}d(x^2-2x+5)\\
=\frac{1}{2}.\frac{(x^2-2x+5)^{\frac{-1}{2}+1}}{\frac{-1}{2}+1}+C=\sqrt{x^2-2x+5}+C\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
Cho
F
x
-
1
3
x
3
là một nguyên hàm của hàm số
f
x
x
. Tìm nguyên hàm của hàm số f(x)lnx. A.
∫
f
x
d
x...
Đọc tiếp
Cho F x = - 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f'(x)lnx.
A. ∫ f ' x d x = ln x x 3 + 1 3 x 3 + C
B. ∫ f ' x d x = - ln x x 3 + 1 3 x 3 + C
C. ∫ f ' x d x = - ln x x 3 + 1 5 x 3 + C
D. ∫ f ' x d x = ln x x 3 + 1 5 x 3 + C
Cho biết hàm số f(x) có đạo hàm f(x) liên tục và có một nguyên hàm là hàm số F(x). Tìm nguyên hàm
Đọc tiếp
Cho biết hàm số f(x) có đạo hàm f'(x) liên tục và có một nguyên hàm là hàm số F(x). Tìm nguyên hàm
![]()
![]()
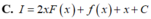
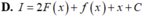
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
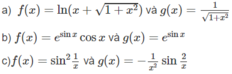
Cho F(x)
1
2
x
2
là 1 nguyên hàm của hàm số
f
(
x
)
x
. Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
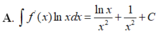
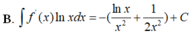
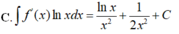
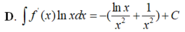
Cho
F
(
x
)
x
2
là một nguyên hàm của hàm số
f
(
x
)
e
2
x
. Tìm nguyên hàm của hàm số
f
(
x
)
e
2
x
Đọc tiếp
Cho F ( x ) = x 2 là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
![]()
![]()
![]()
![]()
Cho
F
(
x
)
-
1
3
x
3
là một nguyên hàm của hàm số
f
(
x
)
x
Tìm nguyên hàm của hàm số f(x)lnx
Đọc tiếp
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
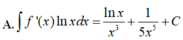
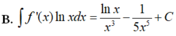
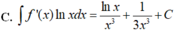
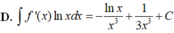
Cho
F
(
x
)
(
x
-
1
)
e
x
là một nguyên hàm của hàm số
f
(
x
)
e
2
x
. Tìm nguyên hàm của hàm số
f
(
x
)
e
2
x
Đọc tiếp
Cho F ( x ) = ( x - 1 ) e x là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
![]()
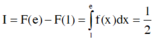
![]()
![]()
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f
x
sin
2
1
x
và
g
x
-
1
x
2
sin
2...
Đọc tiếp
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f x = sin 2 1 x và g x = - 1 x 2 sin 2 x
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f x = e sinx cosx và g x = e sinx
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f
x
ln
x
+
1
+
x
2
và
g
x...
Đọc tiếp
Kiểm tra xem nguyên hàm nào là một nguyên hàm của hàm số còn lại trong mỗi cặp hàm số sau:
f x = ln x + 1 + x 2 và g x = 1 1 + x 2