Đáp án B
Cạnh đáy của khối tám mặt là a 2 + a 2 2 = a 2 2 ⇒ diện tích đáy của khối tám mặt là:
S = a 2 2 2 = a 2 2
Thể tích của khối tám mặt là: V = 2. 1 3 . a 2 . a 2 2 = a 3 6
Đáp án B
Cạnh đáy của khối tám mặt là a 2 + a 2 2 = a 2 2 ⇒ diện tích đáy của khối tám mặt là:
S = a 2 2 2 = a 2 2
Thể tích của khối tám mặt là: V = 2. 1 3 . a 2 . a 2 2 = a 3 6
Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a . Thể tích khối tám mặt đều đó bằng
A. a 3 6
B. a 3 12
C. a 3 4
D. a 3 8
Khối tám mặt đều có đỉnh là tâm các mặt phẳng của hình lập phương cạnh a có thể tích là
![]()
![]()
![]()
![]()
Cho khối tám mặt đều cạnh a. Nối tâm của các mặt bên ta được khối lập phương có thể tích bằng V. Tỷ số a 3 V gần nhất với giá trị nào trong các giá trị sau?
A. 9,5
B. 7,8
C. 15,6
D. 22,6
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh a là
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Cho một khối lập phương có cạnh bằng a. Tính theo a thể tích của khối bát diện đều có các đỉnh là tâm các mặt của khối lập phương.
A. a 3 4
B. a 3 6
C. a 3 12
D. a 3 8
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh bằng 1 là:
A. 1 27
B. 16 2 27
C. 8 27
D. 2 2 27
Tính thể tích khối cầu nội tiếp hình lập phương cạnh a (khối cầu tiếp xúc với tất cả các mặt của hình lập phương).
A. π a 3 2 6
B. π a 3 6
C. π a 3 8
D. π a 3 6
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
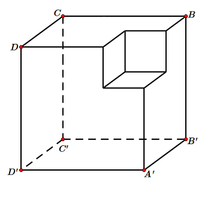
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2