
Gọi bán kính đáy của vật N1 và vật N2 lần lượt là r 1 r 2 .
Khi đó ta có:
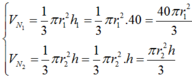
Theo đề bài ta có:
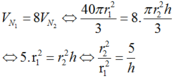
Do cắt vật N1 bằng một mặt cắt song song với mặt đáy nên theo định lý Ta-lét ta có:
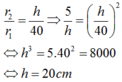
Chọn B.

Gọi bán kính đáy của vật N1 và vật N2 lần lượt là r 1 r 2 .
Khi đó ta có:
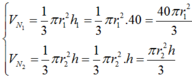
Theo đề bài ta có:
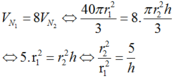
Do cắt vật N1 bằng một mặt cắt song song với mặt đáy nên theo định lý Ta-lét ta có:
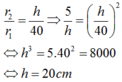
Chọn B.
Cho hình nón N 1 có chiều cao bằng 40cm. Người ta hình nón N 1 bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ N 2 có thể tích bằng 1 8 thể tích N 1 . Tính chiều cao h của hình nón N 2
A. 40cm.
B. 10cm
C. 20cm.
D. 5cm.
Cho hình nón N 1 có chiều cao bằng 40cm. Người ta hình nón N 1 bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ N 2 có thể tích bằng 1 8 thể tích N 1 . Tính chiều cao h của hình nón N 2
A. 40 cm
B. 10 cm
C. 20 cm
D. 5 cm
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của hình nón đỉnh S đáy là hình tròn tâm O' là. (biết thể tích của nó bằng 1/8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O).
A. h=5
B. h=10
C. h=20
D. h=40
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O' bằng bao nhiêu, biết rằng thể tích của nó bằng 1 8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O.
A. h = 5
B. h = 10
C. h = 20
D. h= 40
Cho một hình nón đỉnh S có chiều cao bằng 8cm, bán kính đáy bằng 6cm. Cắt hình nón đã cho bởi một mặt phẳng song song với mặt phẳng chứa đáy được một hình nón (N) đỉnh S có đường sinh bằng 4cm. Tính thể tích của khối nón (N).
A. 768 125 π cm 3
B. 786 125 π cm 3
C. 2304 125 π cm 3
D. 2358 125 π cm 3
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đây
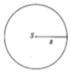
Cách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón N 1
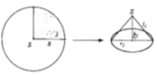
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón N 2
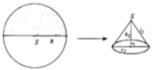
Gọi V 1 , V 2 lần lượt là thể tích của khối nón N 1 và khối nón N 2 . Tính V 1 V 2
A. V 1 V 2 = 9 3 4 2
B. V 1 V 2 = 3 3 2 2
C. V 1 V 2 = 7 2 3
D. V 1 V 2 = 9 7 8 3
Cho hai khối nón ( N 1 ),( N 2 ) . Chiều cao khối nón ( N 2 ) bằng hai lần chiều cao khối nón ( N 1 ) và đường sinh khối nón ( N 2 ) bằng hai lần đường sinh khối nón ( N 1 ). Gọi V 1 , V 2 lần lượt là thể tích hai khối nón ( N 1 ), ( N 2 ). Tỉ số bằng V 1 V 2
A. 1 6
B. 1 8
C. 1 16
D. 1 4
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L). Dựng hình trụ có một đáy là đường tròn (L), một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất
A. x = h 2
B. x = h 3
C. x = h 4
D. x = h
Khi cắt hình nón có chiều cao 16 cm và đường kính đáy 24 cm bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện là một hình Parabol có diện tích lớn nhất bằng

A. 120 2 c m 2
B. 120 6 c m 2
C. 120 3 c m 2
D. 150 3 c m 2