Đáp án A.
Gọi r là bán kính của hình trụ. Ta có V = πr 2 h
Theo giả thiết h = 3, V = 12
π
. Ta có: ![]()
=> Diện tích xung quanh là S = 2 π rl = 12 π
Đáp án A.
Gọi r là bán kính của hình trụ. Ta có V = πr 2 h
Theo giả thiết h = 3, V = 12
π
. Ta có: ![]()
=> Diện tích xung quanh là S = 2 π rl = 12 π
Trong các khối trụ có cùng diện tích toàn phần bằng π . Gọi (T) là khối trụ có thể tích lớn nhất, chiều cao của (T) bằng
![]()
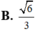
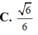
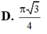
Cho khối trụ có chiều cao h = 3 và diện tích toàn phần bằng 20 π . Khi đó chu vi đáy của khối trụ là
![]()
![]()
![]()
![]()
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
![]()
![]()
![]()
![]()
Một vật thể nằm giữa hai mặt phẳng x = -1 và x = 1 thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x (-1 ≤ x ≤ 1) là một hình tròn có diện tích bằng 3 π Thể tích của vật thể bằng
A. 3 π 2
B. 6 π
C. 6
D. 2 π
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
Phương trình sin 3 x 3 = sin 5 x 5 có 3 nghiệm phân biệt A,B,C thuộc nửa khoảng [0; π ) khi đó cosA+cosB+cosC bằng:
A. 0
B. 1 3
C.- 4 3
D.1
Phương trình sin 3 x 3 = sin 5 x 5 có 3 nghiệm phân biệt A, B, C thuộc nửa khoảng [ 0 ; π ) khi đó cosA + cosB + cosC bằng:
A. 0
B. 1 3
C. - 4 3
D. 1
Cho cos2α=1/4
Tính A=cos(α+π/6)cos(α-π/6)