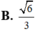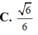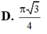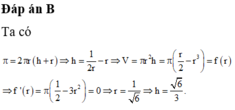Các câu hỏi tương tự
Trong các khối trụ cùng có diện tích toàn phần là
6
π
.
Tìm bán kính đáy của khối trụ có thể tích lớn nhất A.
R
1
B.
R
1
3
C.
R
1
3
D.
R
...
Đọc tiếp
Trong các khối trụ cùng có diện tích toàn phần là 6 π . Tìm bán kính đáy của khối trụ có thể tích lớn nhất
A. R = 1
B. R = 1 3
C. R = 1 3
D. R = 3
Cho khối trụ có chiều cao h 3 và diện tích toàn phần bằng 20
π
. Khi đó chu vi đáy của khối trụ là
Đọc tiếp
Cho khối trụ có chiều cao h = 3 và diện tích toàn phần bằng 20 π . Khi đó chu vi đáy của khối trụ là
![]()
![]()
![]()
![]()
Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng
8
πR
2
. Tính thể tích V của khối trụ (T)
A
.
V
6
πR
3
B
.
V
3
πR
3
C
.
V
...
Đọc tiếp
Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng 8 πR 2 . Tính thể tích V của khối trụ (T)
A . V = 6 πR 3
B . V = 3 πR 3
C . V = 4 πR 3
D . V = 8 πR 3
Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng R. Tính thể tích V của khối trụ
(
T
)
.
Đọc tiếp
Cho khối trụ (T) có bán kính đáy bằng R và diện tích toàn phần bằng R. Tính thể tích V của khối trụ ( T ) .
![]()
![]()
![]()
![]()
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là:
A
.
h
R
1
B
.
h
R
2
C
.
h
R
...
Đọc tiếp
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là:
A . h R = 1
B . h R = 2
C . h R = 2
C . h R = 1 2
Cho khối lăng trụ đứng ABCD.ABCD có đáy là hình vuông có thể tích là V. Để diện tích toàn phần của lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ bằng
Đọc tiếp
Cho khối lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông có thể tích là V. Để diện tích toàn phần của lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ bằng
![]()
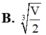
![]()
![]()
Một khối trụ (N) có diện tích xung quanh bằng
4
π
3
và chiều cao là một số nguyên ngoại tiếp một khối nón (N) có đường sinh bằng
7
. Tính thể tích V phần không gian bên ngoài khối nón và bên trong khối trụ.
Đọc tiếp
Một khối trụ (N) có diện tích xung quanh bằng 4 π 3 và chiều cao là một số nguyên ngoại tiếp một khối nón (N') có đường sinh bằng 7 . Tính thể tích V phần không gian bên ngoài khối nón và bên trong khối trụ.
![]()
![]()
![]()
![]()
Cho khối lăng trụ tứ giác đều có cạnh đáy bằng và diện tích toàn phần bằng
8
a
2
.Thể tích khối lăng trụ đó là:
Đọc tiếp
Cho khối lăng trụ tứ giác đều có cạnh đáy bằng và diện tích toàn phần bằng 8 a 2 .Thể tích khối lăng trụ đó là:
![]()
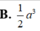
![]()
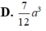
Cho hình lăng trụ tam giác có diện tích đáy bằng 10cm2 và chiều cao bằng 6cm. Thể tích V của khối lăng trụ là
A. V = 20cm3.
B. V = 40cm3.
C. V = 60cm3.
D. V = 80cm3.