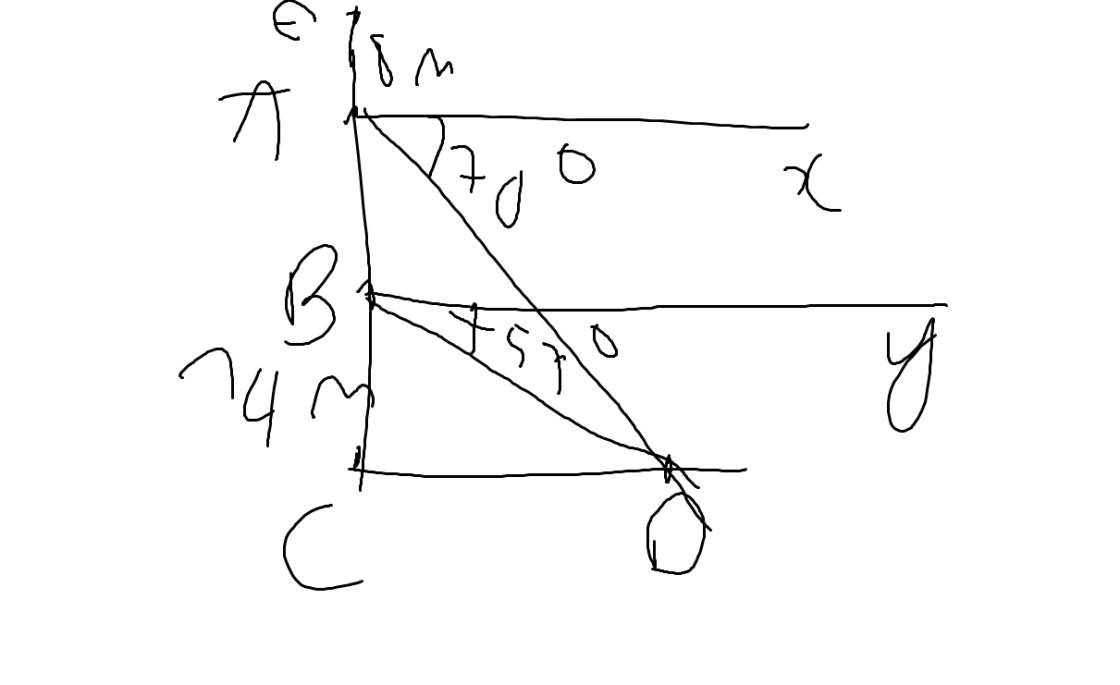
Gọi E là vị trí ban đầu người đó đứng, AC là khoảng cách từ mặt nước đến đáy con tàu bị đắm dưới nước
=>Chiều sâu của con tàu đắm sẽ là EC=EA+AC
Gọi B là vị trí mà người đó lặng xuống sao cho khoảng cách từ điểm đó đến vị trí con tàu đắm là 14m, CD là độ dài của con tàu
Kẻ Ax\(\perp\)EC tại A, By\(\perp\)EC tại B
=>Ax//By
Theo đề, ta có: CD\(\perp\)CE tại C, BE=14m; AE=8m; \(\widehat{xAD}=70^0\); \(\widehat{yBD}=57^0\)
By\(\perp\)EC
CD\(\perp\)EC
Do đó: By//CD
mà By//Ax
nên Ax//By//CD
By//CD
=>\(\widehat{yBD}=\widehat{BDC}\)(hai góc so le trong)
mà \(\widehat{yBD}=57^0\)
nên \(\widehat{BDC}=57^0\)
Xét ΔBCD có \(\widehat{ABD}\) là góc ngoài tại B
nên \(\widehat{ABD}=\widehat{BCD}+\widehat{BDC}=90^0+57^0=147^0\)
\(\widehat{xAD}+\widehat{BAD}=\widehat{xAB}=90^0\)
=>\(\widehat{BAD}=90^0-\widehat{xAD}=90^0-70^0=20^0\)
Xét ΔBAD có \(\widehat{BAD}+\widehat{ABD}+\widehat{ADB}=180^0\)
=>\(\widehat{ADB}=180^0-147^0-20^0=13^0\)
Xét ΔBCD vuông tại C có \(sinBDC=\dfrac{BC}{BD}\)
=>\(\dfrac{14}{BD}=sin57\)
=>\(BD=\dfrac{14}{sin57}\simeq16,69\left(m\right)\)
Xét ΔBAD có \(\dfrac{BD}{sinBAD}=\dfrac{AB}{sinADB}\)
=>\(\dfrac{AB}{sin13}=\dfrac{16.69}{sin20}\)
=>\(AB\simeq10,98\left(m\right)\)
Chiều sâu con tàu đắm là:
EC=EA+AC=8+10,98+14=32,98(m)