Các câu hỏi tương tự
Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn thứ nhất được uốn thành một hình vuông, đoạn thứ hai được uốn thành một vòng tròn. Hỏi khi tổng diện tích của hình vuông và hình tròn ở trên nhỏ nhất thì chiều dài đoạn dây uốn thành hình vuông bằng bao nhiêu (làm tròn đến hàng phần trăm)? A.33,61 cm. B. 26,43 cm C. 40,62 cm D. 30,54 cm
Đọc tiếp
Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn thứ nhất được uốn thành một hình vuông, đoạn thứ hai được uốn thành một vòng tròn. Hỏi khi tổng diện tích của hình vuông và hình tròn ở trên nhỏ nhất thì chiều dài đoạn dây uốn thành hình vuông bằng bao nhiêu (làm tròn đến hàng phần trăm)?
A.33,61 cm.
B. 26,43 cm
C. 40,62 cm
D. 30,54 cm
Một sợi dây không dãn dài 1 mét được cắt thành hai đoạn. Đoạn thứ nhất được cuốn thành đường tròn, đoạn thứ hai được cuốn thành hình vuông. Tính tỉ só độ dài đoạn thứ nhất trên độ dài đoạn thứ hai khi tổng diện tích của hình tròn và hình vuông là nhỏ nhất. A.
π
π
+
4
.
B.
4
π
.
C.1 D.
π
4
.
Đọc tiếp
Một sợi dây không dãn dài 1 mét được cắt thành hai đoạn. Đoạn thứ nhất được cuốn thành đường tròn, đoạn thứ hai được cuốn thành hình vuông. Tính tỉ só độ dài đoạn thứ nhất trên độ dài đoạn thứ hai khi tổng diện tích của hình tròn và hình vuông là nhỏ nhất.
A. π π + 4 .
B. 4 π .
C.1
D. π 4 .
Một sợi dây có chiều dài L (m) được chia thành ba phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai được uốn thành tam giác đều có cạnh gấp hai lần cạnh của hình vuông, phần thứ ba được uốn thành hình tròn (như hình vẽ).Hỏi độ dài cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 3 hình thu được là nhỏ nhất? A.
7
L
49
+...
Đọc tiếp
Một sợi dây có chiều dài L (m) được chia thành ba phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai được uốn thành tam giác đều có cạnh gấp hai lần cạnh của hình vuông, phần thứ ba được uốn thành hình tròn (như hình vẽ).

Hỏi độ dài cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 3 hình thu được là nhỏ nhất?
A. 7 L 49 + 3 + 1 π m
B. 5 L 49 + 3 + 1 π m
C. 5 L 25 + 3 + 1 π m
D. 7 L 25 + 3 + 1 π m
Một sợi dây có chiều 6 mét, được cắt thành hai phần. Phần thứ nhất uốn thành hình tam giác đều, phần thứ hai uốn thành hình vuông. Hỏi cạnh của hình tam giác đều bằng bao nhiêu để tổng diện tích hai hình thu được là nhỏ nhất? A.
12
4
+
3
m
.
B.
36
3
9
+...
Đọc tiếp
Một sợi dây có chiều 6 mét, được cắt thành hai phần. Phần thứ nhất uốn thành hình tam giác đều, phần thứ hai uốn thành hình vuông. Hỏi cạnh của hình tam giác đều bằng bao nhiêu để tổng diện tích hai hình thu được là nhỏ nhất?
A. 12 4 + 3 m .
B. 36 3 9 + 4 3 m .
C. 18 9 + 4 3 m .
D. 18 3 4 + 3 m .
Một sợi dây kim loại dài 32 cm được cắt thành hai đoạn bằng nhau. Đoạn thứ nhất uốn thành một hình chữ nhật có chiều dài 6cm, chiều rộng 2 cm. Đoạn thứ hai uốn thành một tam giác có độ dài một cạnh bằng 6cm. Gọi độ dài hai cạnh còn lại của tam giác là x(cm), y(cm)
x
≤
y
. Hỏi có bao nhiêu cách chọn bộ số (x;y) sao cho diện tích của tam giác không nhỏ hơn diện tích hình chữ nhật? A. 0 cách B. 1 cách C. 2 cách D. Vô s...
Đọc tiếp
Một sợi dây kim loại dài 32 cm được cắt thành hai đoạn bằng nhau. Đoạn thứ nhất uốn thành một hình chữ nhật có chiều dài 6cm, chiều rộng 2 cm. Đoạn thứ hai uốn thành một tam giác có độ dài một cạnh bằng 6cm. Gọi độ dài hai cạnh còn lại của tam giác là x(cm), y(cm) x ≤ y . Hỏi có bao nhiêu cách chọn bộ số (x;y) sao cho diện tích của tam giác không nhỏ hơn diện tích hình chữ nhật?
A. 0 cách
B. 1 cách
C. 2 cách
D. Vô số cách
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của hình hộp chữ nhật và hình trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau? A. 8,3 cm B. 8,4 cm C. 8,5 cm D. 8,6 cm
Đọc tiếp
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của hình hộp chữ nhật và hình trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau?
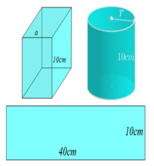
A. 8,3 cm
B. 8,4 cm
C. 8,5 cm
D. 8,6 cm
Một bạn học sinh cắt lấy tờ giấy hình tròn (có bán kính R) rồi cắt một phần giấy có dạng hình quạt. Sau đó bạn ấy lấy phần giấy đó làm thành cái nón chú hề (như hình vẽ). Gọi x là chiều dài dây cung tròn của phần giấy được xếp thành nón chú hề, còn h, r lần lượt là chiều cao và bán kính đáy của của cái nón. Nếu
x
k
.
R
thì giá trị k xấp xỉ bằng bao nhiêu để thể tích của hình nón là lớn nhất. A. 3,15 B. 4,67 C. 5,13 D. 6,35
Đọc tiếp
Một bạn học sinh cắt lấy tờ giấy hình tròn (có bán kính R) rồi cắt một phần giấy có dạng hình quạt. Sau đó bạn ấy lấy phần giấy đó làm thành cái nón chú hề (như hình vẽ). Gọi x là chiều dài dây cung tròn của phần giấy được xếp thành nón chú hề, còn h, r lần lượt là chiều cao và bán kính đáy của của cái nón. Nếu x = k . R thì giá trị k xấp xỉ bằng bao nhiêu để thể tích của hình nón là lớn nhất.
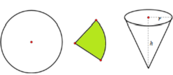
A. 3,15
B. 4,67
C. 5,13
D. 6,35
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của khối hộp chữ nhật và khối trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau? A. 8,3cm. B. 8,4cm. C. 8,5cm. D. 8,6cm.
Đọc tiếp
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của khối hộp chữ nhật và khối trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau?
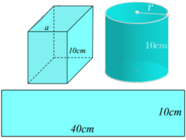
A. 8,3cm.
B. 8,4cm.
C. 8,5cm.
D. 8,6cm.
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất. Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì
a
+
b
là: A.
5
+
5
3...
Đọc tiếp
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất.
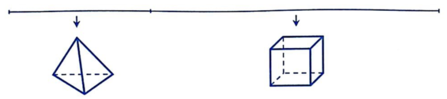
Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a + b là:
A. 5 + 5 3 3
B. - 5 + 5 3 3
C. - 5 + 20 3 3
D. 5 + 20 3 3





