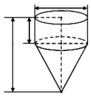
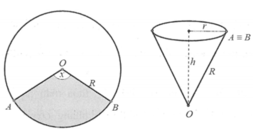
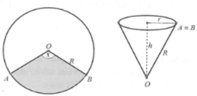
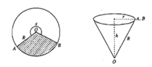
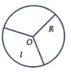
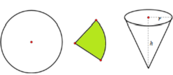
Một bạn học sinh cắt lấy tờ giấy hình tròn (có bán kính R) rồi cắt một phần giấy có dạng hình quạt. Sau đó bạn ấy lấy phần giấy đó làm thành cái nón chú hề (như hình vẽ). Gọi x là chiều dài dây cung tròn của phần giấy được xếp thành nón chú hề, còn h, r lần lượt là chiều cao và bán kính đáy của của cái nón. Nếu x = k . R thì giá trị k xấp xỉ bằng bao nhiêu để thể tích của hình nón là lớn nhất.
A. 3,15
B. 4,67
C. 5,13
D. 6,35
Đáp án C
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13