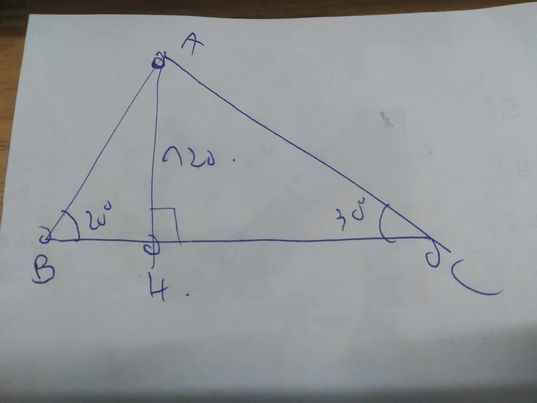
Một người đứng trên tháp ngọn hải đăng cao 120m quan sát hai lần một con thuyền đang di chuyển về phía ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là 200, lần thứ hai người đó nhìn thấy thuyền với góc hạ là 300. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát ? (Làm tròn đến mét)
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát