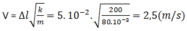Hệ vật ta xét gồm "Quả cầu - Lò xo - Trái Đất" là hệ cô lập.
Cơ năng W của hệ vật này có giá trị bằng tổng của động năng ( W đ ), thế năng trọng trường ( W t ) và thế năng đàn hồi ( W đ h ) :
W = W đ + W t + W đ h
Chọn gốc toạ độ là vị trí cân bằng của hệ vật (quả cầu đứng yên) và chiều dương là chiều lò xo bị kéo dãn. Do đó ta có :
- Tại vị trí ban đầu : hệ vật có W đ = 0 ( v 0 = 0) lò xo bị dãn một đoạn Δ so với vị trí cân bằng, nên W t ≠ 0, W đ h ≠ 0 và cơ năng của hệ vật bằng :
W 0 = 0 + mg ∆ l + k ∆ l + ∆ l 0 2 /2
- Khi về tới vị trí cân bằng : quả cầu có W đ ≠ 0 (v ≠ 0) và W t = 0 (trùng với gốc tính thế năng đàn hồi), đồng thời lò xo bị dãn một đoạn Δ0, nên cơ năng của hệ vật bằng :
W = m v 2 /2 + 0 + k ∆ l 0 2 /2
Chú ý : Hệ vật này được treo thẳng đứng nên tại vị trí cân bằng của nó, lò xo đã bị dãn một đoạn ∆ 0 thoả mãn điều kiện :
mg + k ∆ 0 = 0 ⇒ mg = -k ∆ 0
với P = mg là trọng lực và F đ h = k ∆ là lực đàn hồi tác dụng lên hệ vật
Áp dụng định luật bảo toàn cơ năng cho hệ vật, ta có :
W = W 0 ⇒ mg ∆ l + k ∆ l + ∆ l 0 2 /2 = m v 2 /2 + k ∆ l 0 2 /2
⇒ mg ∆ l + k ∆ l 2 /2 + k ∆ l ∆ l 0 /2 + k ∆ l 0 2 /2 = m v 2 /2 + k ∆ l 0 2 /2
Vì mg = -k ∆ 0 , nên sau khi rút gọn hai vế của phương trình, ta được
k ∆ l 2 /2 = m v 2 /2
Từ đó suy ra vận tốc của quả cầu khi nó về tới vị trí cân bằng: