Các câu hỏi tương tự
Hình trụ (H) có chiều cao bằng
2
a
3
và bán kính đáy bằng
a
3
. Thể tích của khối cầu ngoại tiếp khối trụ là A.
8
6
πa
2
B.
6
6
πa
2
C.
4
6
πa
2...
Đọc tiếp
Hình trụ (H) có chiều cao bằng 2 a 3 và bán kính đáy bằng a 3 . Thể tích của khối cầu ngoại tiếp khối trụ là
A. 8 6 πa 2
B. 6 6 πa 2
C. 4 6 πa 2 3
D. 4 6 πa 2
Một hình trụ có bán kính đáy bằng 1, thiết diện qua trục là hình vuông. Thể tích của khối cầu ngoại tiếp hình trụ là A.
6
π
3
.
B.
3
π
3
.
C.
4
π
2
3
.
D.
8
π...
Đọc tiếp
Một hình trụ có bán kính đáy bằng 1, thiết diện qua trục là hình vuông. Thể tích của khối cầu ngoại tiếp hình trụ là
A. 6 π 3 .
B. 3 π 3 .
C. 4 π 2 3 .
D. 8 π 2 3 .
Một hình trụ có bán kính đáy bằng 1, thiết diện qua trục là hình vuông. Thể tích của khối cầu ngoại tiếp hình trụ là A.
6
π
3
.
B.
3
π
3
.
C.
4
π
2
3
.
D.
8
π
2
3...
Đọc tiếp
Một hình trụ có bán kính đáy bằng 1, thiết diện qua trục là hình vuông. Thể tích của khối cầu ngoại tiếp hình trụ là
A. 6 π 3 .
B. 3 π 3 .
C. 4 π 2 3 .
D. 8 π 2 3 .
Một khối trụ có thể tích bằng 25
π
. Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là: A.
r
10
B.
r
5
C.
r
2
D.
r
15
Đọc tiếp
Một khối trụ có thể tích bằng 25 π . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là:
A. r = 10
B. r = 5
C. r = 2
D. r = 15
Một khối trụ bán kính đáy là
a
3
, chiều cao là
2
a
3
. Tính thể tích khối cầu ngoại tiếp khối trụ. A.
8
6
πa
3
B.
6
6
πa
3
C.
4
3
πa
3
D.
4
6...
Đọc tiếp
Một khối trụ bán kính đáy là a 3 , chiều cao là 2 a 3 . Tính thể tích khối cầu ngoại tiếp khối trụ.
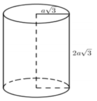
A. 8 6 πa 3
B. 6 6 πa 3
C. 4 3 πa 3
D. 4 6 πa 3 3
Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là: A.
2
πR
3
B.
πR
3
2
2
C.
πR
3
2
6
D.
2
3...
Đọc tiếp
Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là:
A. 2 πR 3
B. πR 3 2 2
C. πR 3 2 6
D. 2 3 πR 3
Cho hình lăng trụ tam giác đều ABC.ABC cạnh đáy bằng a. Biết rằng bán kính mặt cầu ngoại tiếp lăng trụ ABC.ABC bằng a. Tính thể tích V của khối lăng trụ ABC.ABC A.
a
3
2
3
B.
a
3
3
3
C.
a...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' cạnh đáy bằng a. Biết rằng bán kính mặt cầu ngoại tiếp lăng trụ ABC.A'B'C' bằng a. Tính thể tích V của khối lăng trụ ABC.A'B'C'
A. a 3 2 3
B. a 3 3 3
C. a 3 3 2
D. a 3 2 2
Một khối hình trụ có chiều cao bằng 3 lần đường kính của mặt đáy chứa đầy nước. Người ta đặt vào trong khối đó một khối cầu có đường kính bằng đường kính khối trụ và một khối nón có đỉnh tiếp xúc với khối cầu, đáy khối nón trùng với đáy trên của khối trụ (như hình vẽ). Tính tỉ số thể tích của lượng nước còn lại trong khối trụ và lượng nước của khối trụ ban đầu. A.
4
9
B.
5
9
C.
2...
Đọc tiếp
Một khối hình trụ có chiều cao bằng 3 lần đường kính của mặt đáy chứa đầy nước. Người ta đặt vào trong khối đó một khối cầu có đường kính bằng đường kính khối trụ và một khối nón có đỉnh tiếp xúc với khối cầu, đáy khối nón trùng với đáy trên của khối trụ (như hình vẽ).
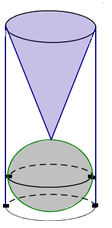
Tính tỉ số thể tích của lượng nước còn lại trong khối trụ và lượng nước của khối trụ ban đầu.
A. 4 9
B. 5 9
C. 2 3
D. 1 2
Cho khối cầu (S) có bán kính R. Một khối trụ có thể tích bằng
4
π
3
9
R
3
và nội tiếp khối cầu (S). Chiều cao khối trụ bằng A.
2
3
3
R
B.
2
2
R
C.
3...
Đọc tiếp
Cho khối cầu (S) có bán kính R. Một khối trụ có thể tích bằng 4 π 3 9 R 3 và nội tiếp khối cầu (S). Chiều cao khối trụ bằng
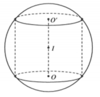
A. 2 3 3 R
B. 2 2 R
C. 3 3 R
D. R 2




