Các câu hỏi tương tự
Một khối lập phương có cạnh 1m. Người ta sơn đỏ tất cả các mặt của khối lập phương rồi cắt khối lập phương bằng các mặt phẳng song song với các mặt của khối lập phương để được 1000 khối lập phương nhỏ có cạnh 10dm. Hỏi các khối lập phương thu được sau khi cắt có bao nhiêu khối lập phương có đúng 2 mặt được sơn đỏ? A. 64 B. 81 C. 100 D. 96
Đọc tiếp
Một khối lập phương có cạnh 1m. Người ta sơn đỏ tất cả các mặt của khối lập phương rồi cắt khối lập phương bằng các mặt phẳng song song với các mặt của khối lập phương để được 1000 khối lập phương nhỏ có cạnh 10dm. Hỏi các khối lập phương thu được sau khi cắt có bao nhiêu khối lập phương có đúng 2 mặt được sơn đỏ?
A. 64
B. 81
C. 100
D. 96
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (ABCD), (BCCB) và (DCCD). Tính bán kính của S.
A
.
2
+
3
3
B
.
3
-...
Đọc tiếp
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
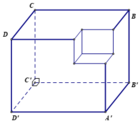
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
A . 2 + 3 3
B . 3 - 3
C . 2 3 3
D . 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, AB và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng A.
10
4
B.
6
3
C. ...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, A'B' và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng
A. 10 4
B. 6 3
C. 6 6
D. 3 3
Cho khối lập phương ABCD.ABCD cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MBDN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:A.
a
3
9
B.
a
3
6
C.
a...
Đọc tiếp
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt đều đó:
Đọc tiếp
Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt đều đó:
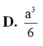
Cho hình lập phương ABCD.ABCD có cạnh bằng
3
. Mặt phẳng
α
cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng
α
biết
α
tạo với mặt (ABBA) một góc
60
0
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 . Mặt phẳng α cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng α biết α tạo với mặt (ABB'A') một góc 60 0 .
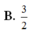
![]()
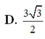
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi E và F lần lượt là trung điểm của B'C' và C'D'. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A'. Tính thể tích của (H).
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi
V
1
là thể tích khối chứa điểm A’ và
V
2
là thể tích khối chứa điểm C’. Khi đó
V
1
V
2
là A.
25
47...
Đọc tiếp
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A’ và V 2 là thể tích khối chứa điểm C’. Khi đó V 1 V 2 là
A. 25 47 .
B. 1
C. 17 25 .
D. 8 17 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm A’B’, N là trung điểm BC. Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A, (H’) là khối đa diện còn lại. Tính tỉ số
V
H
V
H
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm A’B’, N là trung điểm BC. Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A, (H’) là khối đa diện còn lại. Tính tỉ số V H V H '





