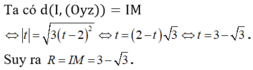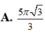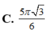Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
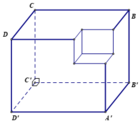
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
A . 2 + 3 3
B . 3 - 3
C . 2 3 3
D . 2
Chọn B
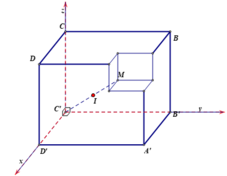
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
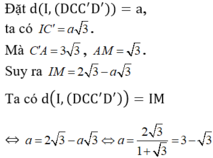
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là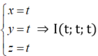 
với 2 > 0 > t do I thuộc đoạn thẳng C'M
