diện tích hình vuông là :
9 x 4 = 36 (cm2)
vậy cạnh của hình vuông là : 6 cm
Diện tích hình vuông là :
9 . 1/4 = 9/4(cm2)
Cạnh hình vuông là :
9/4 :4=9/16(cm)
Đáp số: 9/16 cm
Cho một hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được một hình vuông, tiếp tục làm như thế đối với hình vuông mới (như hình vẽ bên).
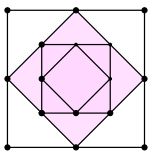
Tổng diện tích cách hình vuông liên tiếp đó là
A. 2
B. 3 2
C. 8
D. 4
Một hình vuông A B C D có cạnh A B = a . , diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh A B , B C , C D , D A ta được một hình vuông thứ hai A 1 , B 1 , C 1 , D 1 có diện tích S 2 . Tiếp tục như vậy ta được hình vuông thứ 3 là có diện tích S 3 và cứ như thế ta được S 4 , S 5 ,... Tính giá trị của S = S 1 + S 2 + S 3 + ... + S 100
A. 2 100 − 1 2 99 a 2
B. a 2 100 − 1 2 99
C. a 2 2 100 − 1 2 99
D. a 2 2 99 − 1 2 99
Một hình vuông ABCD có cạnh A B = a , diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai là A 1 B 1 C 1 D 1 có diện tích S 2 . Tiếp tục như thế ta được hình vuông thứ ba là A 2 B 2 C 2 D 2 có diện tích S 3 và cứ tiếp tục như thế, ta được diện tích S 4 , S 5 , . . .
Tính S = S 1 + S 2 + S 3 + . . . . + S 100
A. S = 2 100 - 1 2 99 a 2
B. S = a 2 100 - 1 2 99
C. S = a 2 2 100 - 1 2 99
D. S = a 2 2 99 - 1 2 99
Cho hình vuông có cạnh là 1. Nối các trung điểm của hình vuông trên ta được một hình vuông có diện tích S 1 tiếp tục quá trình trên với các hình vuông với diện tích là S 1 ; S 3 ; . . . ; S n ; . . . Tính tổng vô hạn S 1 + S 2 + S 3 + . . . + S n + . . .
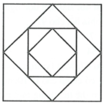
A. 1
B. 1/2
C. 2
D. 3/2
Để trang hoàng cho căn hộ của mình, An quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Bạn ấy tô màu đỏ các hình vuông nhỏ được đánh số lần lượt là 1,2,3,....,n,..., trong đó cạnh của hình vuông kế tiếp bằng một nửa hình vuông trước đó (như hình bên). Giả sử quy trình tô màu của An có thể tạo ra vô hạn. Hỏi bạn An tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô nhỏ hơn 1 1000
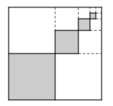
A. 3
B. 4
C. 5
D. 10
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a, AA’ = 2a. Một hình trụ có hai đáy là hai hình tròn lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’. Tính diện tích xung quanh S x q của hình trụ đó
A. S x q = 2 πa 2
B. S x q = 2 πa 2 2
C. S x q = 4 πa 2 2
D. S x q = πa 2 2
Cho hình lập phương có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông ABCD và có đường tròn đáy ngoại tiếp hình vuông AB'C'D'. Diện tích xung quanh của hình nón đó bằng
A. 2 π a 2 2
B. 6 π a 2 2
C. 2 π a 3 2
D. 3 π a 2 2
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông A ' B ' C ' D ' và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón đó.
A. π a 2 2 2
B. π a 2 3
C. π a 2 2 4
D. π a 2 3 2
Cho tam giác ABC vuông tại A có B C = 2 a v à A B C ⏜ = 30 ∘ . Quay tam giác vuông này quanh cạnh AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích xung quanh của hình nón đó và S 2 là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số S 1 S 2 là
A. S 1 S 2 = 1
B. S 1 S 2 = 2 3
C. S 1 S 2 = 1 2
D. S 1 S 2 = 3 2
