Đáp án B
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết dễ suy ra đường tròn đáy có bán kính
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Một hình nón có đường kính đáy là 2 a 3 , góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a
A. 3 πa 3
B. πa 3
C. 2 3 πa 3
D. πa 3 3
Một hình nón có đường kính đáy là 2 a 3 , góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a.
A. 3 πa 3
B. 2 3 πa 3
C. 4 πa 3
D. πa 3
Cho biết I = ∫ 0 π 4 sin x + 3 cos x sin x + cos x d x = πa + lnb (0<a<1; 1<b<3). Tích a.b bằng bao nhiêu?
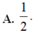
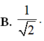
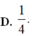
Một hình nón có đường kính đáy là 2 a 3 , góc ở đỉnh là 120 ° . Tính diện tích xung quanh của hình nón theo a
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + ln c b với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + 1 b ln c với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Cho tam giác ABC vuông tại A có BC = 2a và ∠ B = 30 ° . Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích toàn phần của hình nón đó và S 2 là diện tích mặt cầu đường kính AB. Khi đó, tỉ số S 1 / S 2 là:
A. 1 B. 1/2
C. 2/3 D. 3/2
