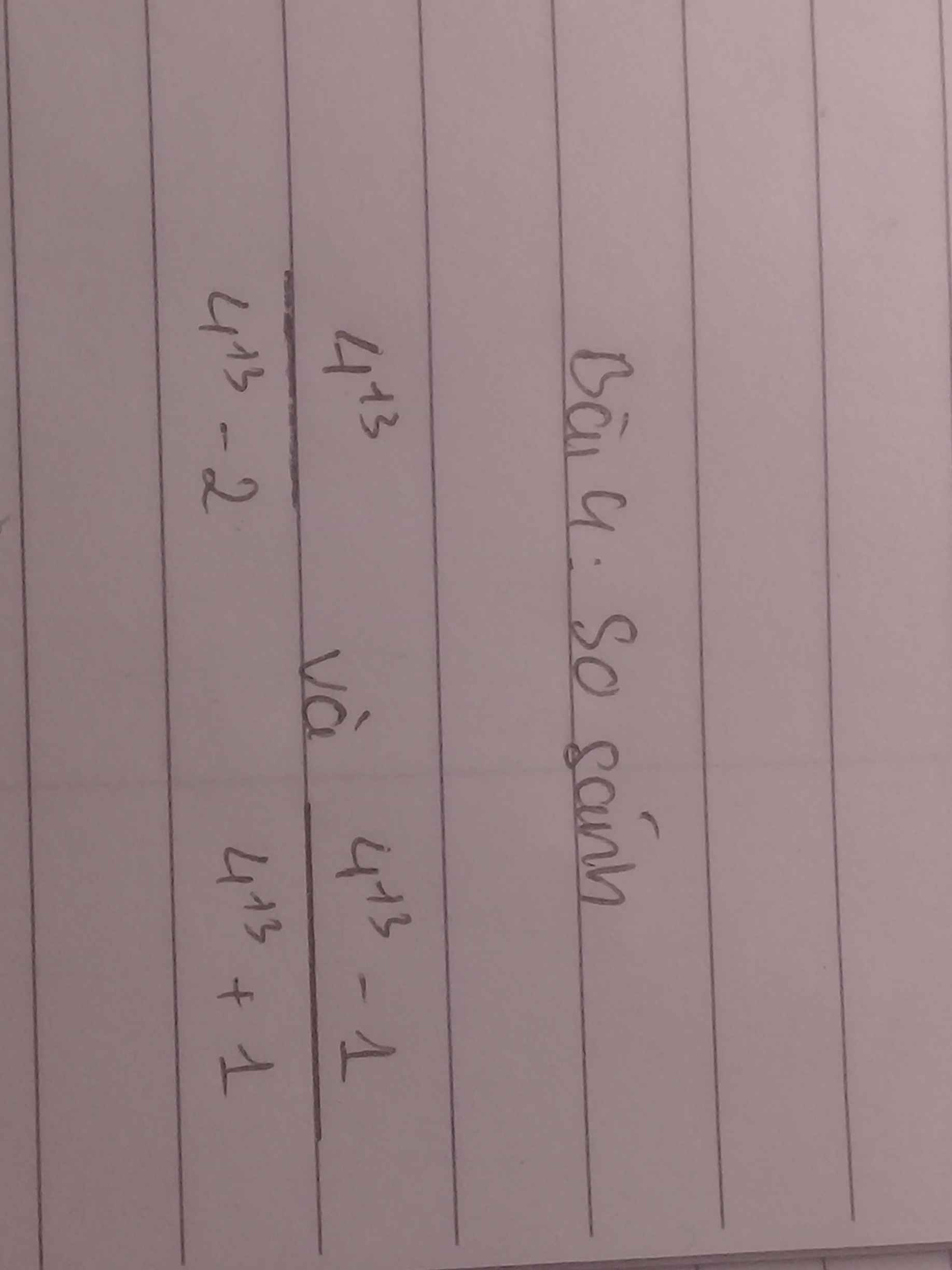Question

mong mn giúp mik, mình cần gấp

Answer 1

\(\dfrac{4^{13}}{4^{13}-2}=1+\dfrac{2}{4^{13}-2}\)

\(\dfrac{4^{13}-1}{4^{13}+1}=1-\dfrac{2}{4^{13}+1}\)

Do \(4^{13}-2< 4^{13}+1\Rightarrow\dfrac{2}{4^{13}-2}>\dfrac{2}{4^{13}+1}\Rightarrow\dfrac{2}{4^{13}-2}>-\dfrac{2}{4^{13}-1}\)

\(\Rightarrow\dfrac{4^{13}}{4^{13}-2}>\dfrac{4^{13}-1}{4^{13}+1}\)

 

Answer 2

Ta có:

\(\dfrac{4^{13}}{4^{13}-2}=\dfrac{4^{13}-2}{4^{13}-2}+\dfrac{2}{4^{13}-2}=1+\dfrac{2}{4^{13}-2}\)

\(\dfrac{4^{13}-1}{4^{13}+1}=\dfrac{4^{13}+1}{4^{13}+1}-\dfrac{2}{4^{13}+1}=1-\dfrac{2}{4^{13}+1}\)

Vì \(1+\dfrac{2}{4^{13}-2}>1-\dfrac{2}{4^{13}+1}\)

⇒\(\dfrac{4^{13}}{4^{13}-2}>\)\(\dfrac{4^{13}-1}{4^{13}+1}\)