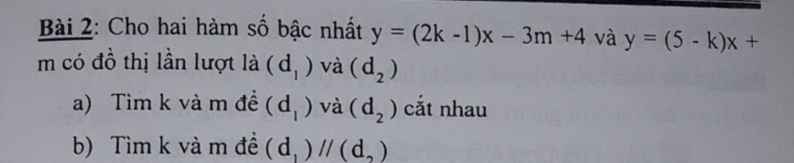Hướng dẫn:
a. Em tự giải
b.
Do \(\left\{{}\begin{matrix}BK||AH\\AH\perp BC\end{matrix}\right.\) \(\Rightarrow BK\perp BC\) hay tam giác BCK vuông tại B
Áp dụng hệ thức lượng cho tam giác vuông BCK với đường cao BA:
\(BK^2=KA.KC\)
c.
Ta có tứ giác AMBH là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow\widehat{BMH}=\widehat{BAH}\)
Mà \(\widehat{BAH}=\widehat{ACB}\) (cùng phụ \(\widehat{ABC}\))
\(\Rightarrow\widehat{BMH}=\widehat{ACB}\)
\(\Rightarrow\Delta_VBMH\sim\Delta_VBCK\left(g.g\right)\)
\(\dfrac{S_{BMH}}{S_{BCK}}=\dfrac{\dfrac{1}{2}BM.BH}{\dfrac{1}{2}BK.BC}=\left(\dfrac{BH}{BC}\right).\left(\dfrac{BM}{BK}\right)=\left(\dfrac{BH.BC}{BC^2}\right).\left(\dfrac{BM.BK}{BK^2}\right)\)
\(=\left(\dfrac{AB^2}{BC^2}\right)\left(\dfrac{AB^2}{BK^2}\right)=sin^2C.sin^2K\)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
