Ta có: \(a+b=2\Rightarrow a=2-b\)
\(\dfrac{4}{a+3}+\dfrac{4}{b+3}\)
\(=\dfrac{4}{2-b+3}+\dfrac{4}{b+3}\)
\(=\dfrac{4}{5-b}+\dfrac{4}{b+3}\)
\(=\dfrac{4\left(b+3\right)}{\left(5-b\right)\left(b+3\right)}+\dfrac{4\left(5-b\right)}{\left(5-b\right)\left(b+3\right)}\)
\(=\dfrac{4b+12+20-4b}{5b+15-b^2-3b}\)
\(=\dfrac{32}{-\left(b^2-2b-15\right)}\)
\(=\dfrac{32}{-\left[b^2-2b+1-16\right]}\)
\(=\dfrac{32}{-\left(b-1\right)^2+16}\)
Mà: \(-\left(b-1\right)^2+16\le16\)
\(\Rightarrow\dfrac{32}{-\left(b-1\right)^2+16}\ge\dfrac{32}{16}=2\)
Dấu "=" xảy ra:
\(\dfrac{32}{-\left(b-1\right)^2+16}=2\)
\(\Rightarrow-\left(b-1\right)^2=0\)
\(\Rightarrow b=1\)
\(\Rightarrow a=2-1=1\)
Vậy \(GTNN\) là \(2\) khi \(a=b=1\)

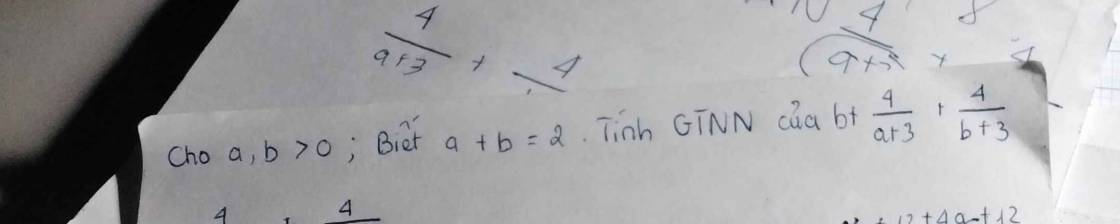




 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)