Lời giải:
1. Gọi $O$ là trung điểm $AH$. Hay $O$ chính là tâm đường tròn đường kính $AH$.
Ta thấy $OK=OI=R$ và $O,K,I$ thẳng hàng nên $O$ là trung điểm $KI$
Tứ giác $AKHI$ có 2 đường chéo $KI, AH$ cắt nhau tại trung điểm $O$ của mỗi đường nên $AKHI$ là hbh.
Mà $\widehat{A}=90^0$ nên $AKHI$ là hcn.
2.
Vì $AKHI$ là hcn nên $\widehat{AKI}=\widehat{AHI}(1)$
Cũng vì $AKHI$ là hcn nên $\widehat{HIA}=90^0$
$\Rightarrow \widehat{AHI}=90^0-\widehat{HAI}=90^0-\widehat{HAC}=\widehat{HCA}=\widehat{BCI}(2)$
Từ $(1); (2)\Rightarrow \widehat{AKI}=\widehat{BCI}$
$\Rightarrow BKIC$ là tgnt.
3.
Vì $HN\perp OH$ nên $HN$ là tiếp tuyến tại $H$ của đường tròn $(O)$
Xét tam giác $NHK$ và $NIH$ có:
$\widehat{N}$ chung
$\widehat{NHK}=\widehat{NIK}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nt chắn cung đó - ở đây là cung $KH$)
$\Rightarrow \triangle NHK\sim \triangle NIH$ (g.g)
$\Rightarrow \frac{NH}{NK}=\frac{NI}{NH}\Rightarrow NH^2=NK.NI$
4. Gọi $T$ là giao điểm $AM$ và $IK$
Vì $AM$ là trung tuyến ứng với cạnh huyền của tam giác vuông $ABC$ nên $AM=\frac{BC}{2}=AC$
$\Rightarrow \widehat{MAC}=\widehat{MCA}$ hay $\widehat{TAI}=\widehat{HCA}(3)$
Vì $AKHI$ là hcn nên:
$\widehat{TIA}=\widehat{OIA}=\widehat{OAI}=\widehat{HAC}(4)$
Từ $(3); (4)\Rightarrow \widehat{TAI}+\widehat{TIA}=\widehat{HCA}+\widehat{HAC}=90^0$
$\Rightarrow TIA$ là tam giác vuông tại $T$
$\Rightarrow AM\perp IK$
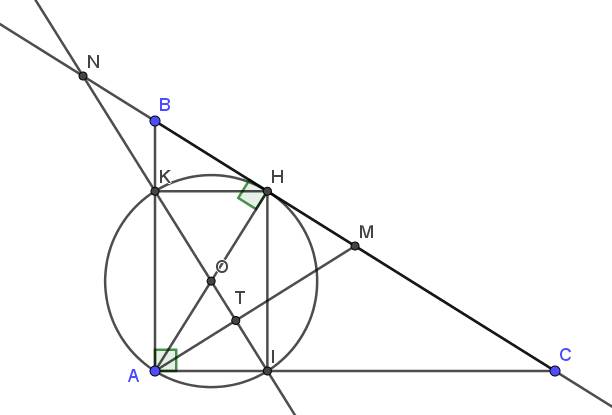
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
