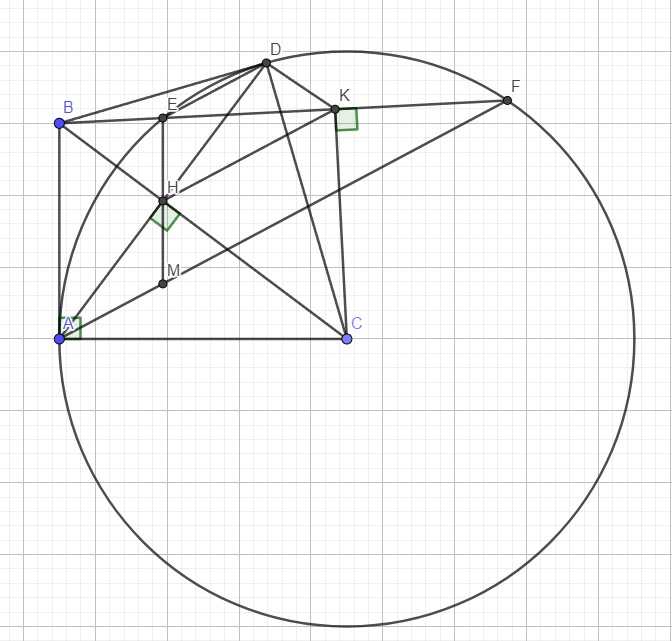
BD là tiếp tuyến (C) nên \(\widehat{BDC}=90^0\)
K là trung điểm EF nên \(\widehat{BKC}=90^0\)
\(\Rightarrow D;K\) cùng nhìn BC dưới 1 góc vuông nên BDKC nội tiếp
\(\Rightarrow\widehat{DKB}=\widehat{DCB}\)
Mà \(\widehat{DCB}=\dfrac{1}{2}\widehat{DCA}\) ; \(\widehat{DAB}=\dfrac{1}{2}\widehat{DCA}\) \(\Rightarrow\widehat{DKB}=\widehat{DAB}\)
Lại có EH song song AB (gt) \(\Rightarrow\widehat{DAB}=\widehat{DHE}\) (đồng vị)
\(\Rightarrow\widehat{DKB}=\widehat{DHE}\)
2 góc nói trên cùng nằm ở nửa mp bờ EH và cùng chắn EH \(\Rightarrow DEHK\) nội tiếp
\(\Rightarrow\widehat{HDE}=\widehat{HKE}\)
Mà \(\widehat{HDE}=\widehat{AFE}\) (cùng chắn AE của (C))
\(\Rightarrow\widehat{HKE}=\widehat{AFE}\Rightarrow HK||AF\) (hai góc đồng vị bằng nhau)
Gọi M là giao điểm AF và EH. Trong tam giác EMF, có HK qua trung điểm cạnh bên EF và song song cạnh đáy AF
\(\Rightarrow HK\) là đường trung bình tam giacs EMF \(\Rightarrow H\) là trung điểm EM
\(\Rightarrow EH=HM\)
Xét 2 tam giác HED và HMA có:
\(\left\{{}\begin{matrix}HE=HM\left(cmt\right)\\\widehat{EHD}=\widehat{MHA}\left(\text{đối đỉnh}\right)\\HA=HD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta HED=\Delta HMA\left(c.g.c\right)\)
\(\Rightarrow\widehat{HDE}=\widehat{HAM}\Rightarrow ED||AF\) (hai góc slt bằng nhau)
\(\Rightarrow AF||ED||HK\)
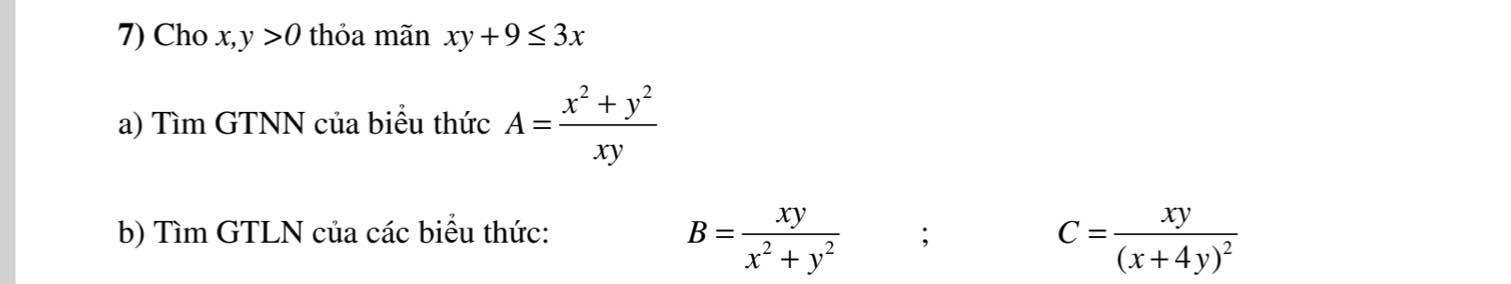mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
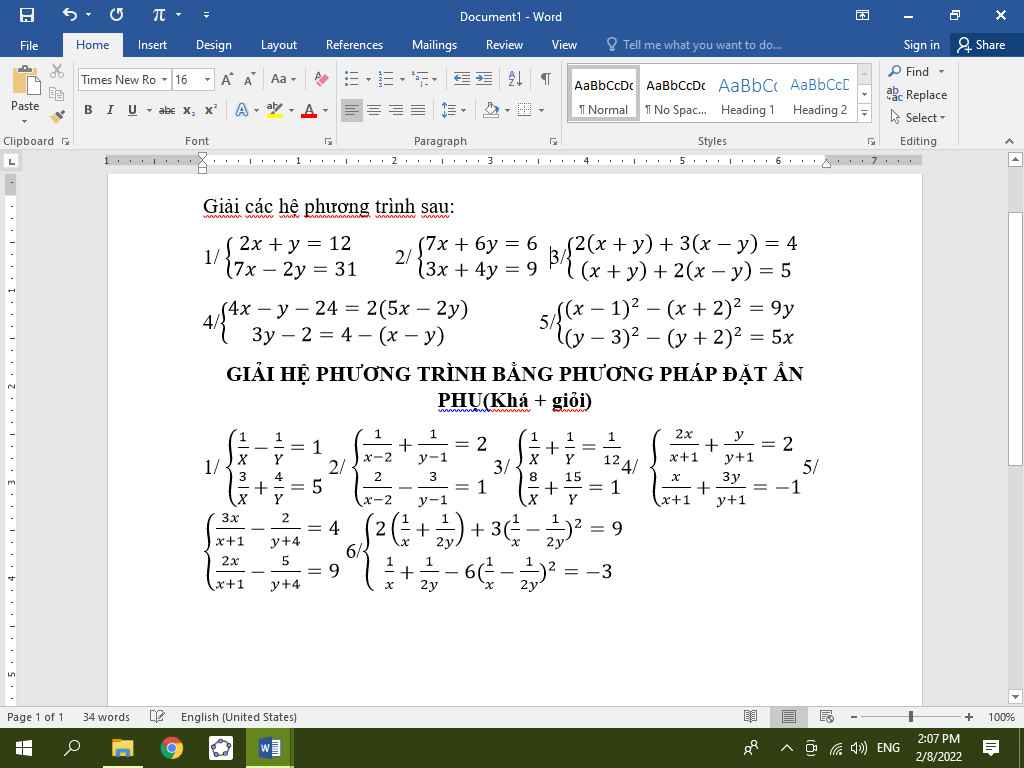
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
