câu 12:
Sử dụng quỹ tích điểm:
\(T_{\overrightarrow{V}}\left(M\right)=M'\left(X';Y'\right)\) với mọi điểm \(M\left(x';y'\right)\in\left(E\right)\Rightarrow\left\{{}\begin{matrix}X=X'-2\\Y=Y'-2\end{matrix}\right.\)
\(\left(E\right):\dfrac{\left(x-2\right)^2}{16}+\dfrac{\left(y-1\right)^2}{9}=1\)
câu 13;
\(\text{✳}d=MN=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
\(\text{✳}d'=M'N'=\sqrt{\left(X'_2-X'_1\right)^2+\left(Y'_2-Y'_1\right)^2}\)
✱\(\left(X'_2-X'_1\right)^2\)
\(=\left[\left(X_2-X_1\right)\cos a+\left(-Y_2+Y_1\right)\sin a\right]^2\)
\(=\left[\left(X_2-X_1\right)\cos a-\left(Y_2-Y_1\right)\sin a\right]^2\)
\(=\left(X_2-X_1\right)^2\cos^2a+\left(Y_2-Y_1\right)^2\sin^2a-2\left(X_2-X_1\right)\left(Y_2-Y_1\right)\sin a.\cos a\)
✱\(\left(Y'_2-Y'_1\right)^2\)
\(=\left[\left(X_2-X_1\right)\sin a-\left(Y_2-Y_1\right)\cos a\right]^2\)
\(=\left(X_2-X_1\right)^2\sin^2a+\left(Y_2-Y_1\right)^2\cos^2a-2\left(X_2-X_1\right)\left(Y_2-Y_1\right)\sin a.\cos a\)
vậy \(d'=\sqrt{=\left(X_2-X_1\right)^2\left(\cos^2a+\sin^2a\right)+\left(Y_2-Y_1\right)^2\left(\sin^2a+\cos^2a\right)}\)
HAY \(d'=\sqrt{\left(X_2-X_1\right)^2+\left(Y_2-Y_1\right)^2}\) (vì \(\cos^2a+\sin^2a=1\))

















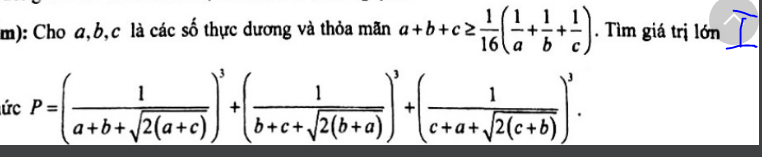 mọi người giúp em với em cảm ơn nhiều lắmmmmm
mọi người giúp em với em cảm ơn nhiều lắmmmmm




