Bài 4:
a: Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(\dfrac{4}{12}=\dfrac{5}{12}\right)\)
nên DE//BC
Xét ΔABC có DE//BC
nên ΔADE~ΔABC
b: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Xét ΔCEF và ΔEAD có
\(\widehat{CEF}=\widehat{EAD}\)(hai góc đồng vị, EF//AB)
\(\widehat{CFE}=\widehat{EDA}\left(=\widehat{ABC}\right)\)
Do đó: ΔCEF~ΔEAD
Bài 5:
ĐKXĐ: \(x\notin\left\{-1;-2;...;-13\right\}\)
\(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}+...+\dfrac{1}{x^2+25x+156}=\dfrac{3}{91}\)
=>\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+...+\dfrac{1}{\left(x+12\right)\left(x+13\right)}=\dfrac{3}{91}\)
=>\(\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+...+\dfrac{1}{x+12}-\dfrac{1}{x+13}=\dfrac{3}{91}\)
=>\(\dfrac{1}{x+1}-\dfrac{1}{x+13}=\dfrac{3}{91}\)
=>\(\dfrac{x+13-x-1}{\left(x+1\right)\left(x+13\right)}=\dfrac{3}{91}\)
=>\(\dfrac{4}{\left(x+1\right)\left(x+13\right)}=\dfrac{1}{91}\)
=>\(\left(x+1\right)\left(x+13\right)=4\cdot91=364\)
=>\(x^2+14x+13-364=0\)
=>\(x^2+14x-351=0\)
=>(x-13)(x+27)=0
=>\(\left[{}\begin{matrix}x=13\left(nhận\right)\\x=-27\left(nhận\right)\end{matrix}\right.\)
1.
a. ĐKXĐ: \(x\ne\left\{-1;0\right\}\)
\(\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{x+1}{x\left(x+1\right)}-\dfrac{x}{x\left(x+1\right)}=\dfrac{x+1-x}{x\left(x+1\right)}=\dfrac{1}{x\left(x+1\right)}\)
b.
\(5+2x=x-5\)
\(\Leftrightarrow2x-x=-5-5\)
\(\Leftrightarrow x=-10\)
2.
a. Em tự vẽ
b.
Để đường thẳng song song với \(y=-x+2\)
\(\Rightarrow\left\{{}\begin{matrix}m-1=-1\\m+4\ne2\end{matrix}\right.\)
\(\Rightarrow m=0\)
3.
Gọi độ dài quãng đường AB là x (km) với x>0
Thời gian ô tô đi từ A đến B là: \(\dfrac{x}{50}\) giờ
Thời gian ô tô đi từ B về A là: \(\dfrac{x}{60}\) giờ
Do thời gian về ít hơn thời gian đi là 30 phút =1/2 giờ nên ta có pt:
\(\dfrac{x}{50}-\dfrac{x}{60}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{x}{300}=\dfrac{1}{2}\)
\(\Leftrightarrow x=150\left(km\right)\)
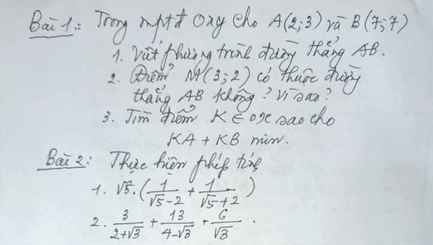làm hộ mik bài 1 thôi nha
