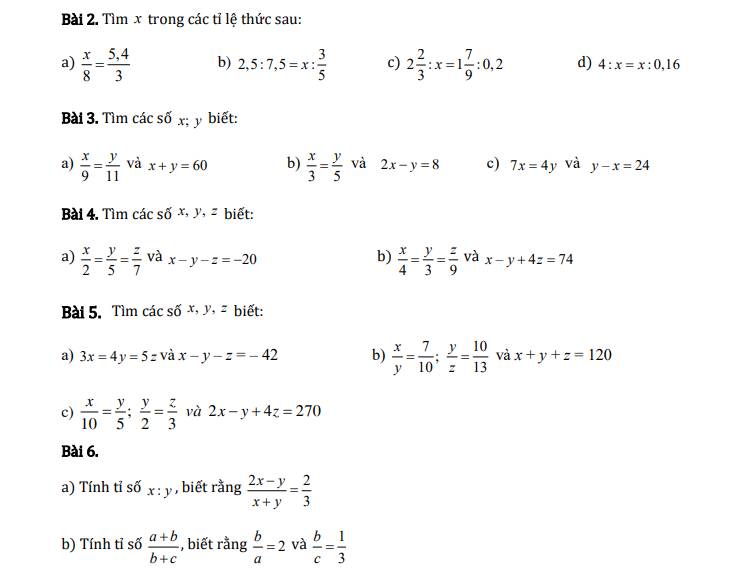Bài 2
a) x/8 = 5,4/3
x = 8 . 5,4/3
x = 14,4
b) 2,5 : 7,5 = x : 3/5
x = 3/5 × 1/3
x = 1/5
c) 2 2/3 : x = 1 7/9 : 0,2
8/3 : x = 16/9 : 1/5
x = 8/3 : (16/9 : 1/5)
x = 8/3 : 80/9
x = 3/10
d) 4/x = x/0,16
x² = 4 . 0,16
x² = 0,64
x = 0,8 hoặc x = -0,8
Bài 3
a) x/9 = y/11 và x + y = 60
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/9 + y/11 = (x + y)/(9 + 11) = 60/20 = 3
x/9 = 3 ⇒ x = 9.3 = 27
y/11 = 3 ⇒ y = 11.3 = 33
Vậy x = 27; y = 33
b) x/3 = y/5 ⇒ 2x/6 = y/5 và 2x - y = 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/6 = y/5 = (2x - y)/(6 - 5) = 8/1 = 8
2x/6 = 8 ⇒ x = 6.8:2 = 24
y/5 = 8 ⇒ y = 5.8 = 40
Vậy x = 24; y = 40
c) 7x = 4y ⇒ y/7 = x/4 và y - x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
y/7 = x/4 = (y - x)/(7 - 4) = 24/3 = 8
x/4 = 8 ⇒ x = 4.8 = 32
y/7 = 8 ⇒ y = 7.8 = 56
Vậy x = 32; y = 56
Bài 4
a) x/2 = y/5 = z/7 và x - y - z = -20
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/2 = y/5 = z/7 = (x - y - z)/(2 - 5 - 7) = -20/(-10) = 2
x/2 = 2 ⇒ x = 2.2 = 4
y/5 = 2 ⇒ y = 5.2 = 10
z/7 = 2 z = 7.2 = 14
Vậy x = 4; y = 10; z = 14
b) x/4 = y/3 = z/9 ⇒ x/4 = y/3 = 4z/36
Và x - y + 4z = 74
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/4 = y/3 = 4z/36 = (x - y + 4z)/(4 - 3 + 36) = 74/37 = 2
x/4 = 2 ⇒ x = 4.2 = 8
y/3 = 2 ⇒ y = 3.2 = 6
z/9 = 2 ⇒ z = 9.2 = 18
Vậy x = 8; y = 6; z = 18
Bài 5
a) 3x = 4y = 5z ⇒ x/(1/3) = y/(1/4) = z/(1/5)
Và x - y - z = -42
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/(1/3) = y/(1/4) = z/(1/5) = (x - y - z)/(1/3 - 1/4 - 1/5) = -42/(-7/60) = 360
3x = 360 ⇒ x = 360 : 3 = 120
4y = 360 ⇒ y = 360 : 4 = 90
5z = 360 ⇒ z = 360 : 5 = 72
Vậy x = 120; y = 90; z = 72
b) x/y = 7/10 x/7 = y/10 (1)
y/z = 10/13 y/10 = z/13 (2)
Từ (1) và (2) ⇒ x/7 = y/10 = z/13
Và x + y + z = 120
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/7 = y/10 = z/13 = (x + y + z)/(7 + 10 + 13) = 120/30 = 4
x/7 = 4 ⇒ x = 7.4 = 28
y/10 = 4 ⇒ y = 10.4 = 40
z/13 = 4 ⇒ z = 13.4 = 52
Vậy x = 28; y = 40; z = 52
c) x/10 = y/5 ⇒ x/20 = y/10 ⇒ 2x/40 = y/10 (1)
y/2 = z/3 ⇒ y/10 = z/15 ⇒ y/10 = 4z/60 (2)
Từ (1) và (2) ⇒ 2x/40 = y/10 = 4z/60
Và 2x - y + 4z = 270
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/40 = y/10 = 4z/60 = (2x - y + 4z)/(40 - 10 + 60) = 270/90 = 3
2x/40 = 3 ⇒ x = 3.40:2 = 60
y/10 = 3 ⇒ y = 10.3 = 30
4z/60 = 3 ⇒ z = 3.60:4 = 45
Vậy x = 60; y = 30; z = 45
Bài 6
a) (2x - y)/(x + y) = 2/3
⇒ 3(2x - y) = 2(x + y)
⇒ 6x - 3y = 2x + 2y
⇒ 6x - 2x = 2y + 3y
⇒ 4x = 5y
⇒ x : y = 5 : 4
b) b/a = 2 ⇒ a = b/2
b/c = 1/3
⇒ c = 3b
⇒ (a + b)/(b + c) = (b/2 + b)/(b + 3b)
= (3b/2)/(4b)
= 3/8
Vậy (a + b)/(b + c) = 3/8