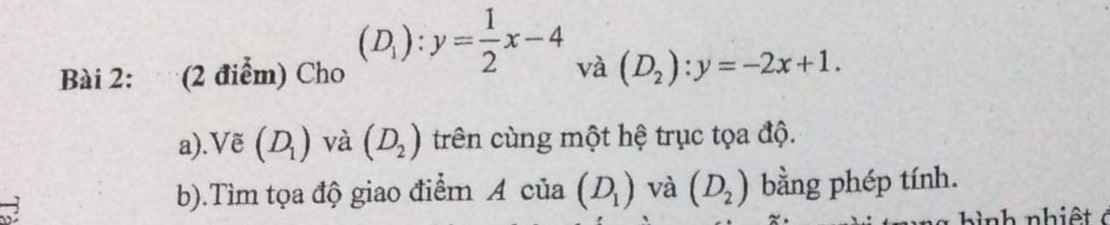1: \(B=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{15-\sqrt{x}+2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\sqrt{x}+5}\cdot\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{1+\sqrt{x}}{\sqrt{x}+1}\)
=1
2: \(A=\left(\dfrac{x}{\sqrt{x}-2}-\dfrac{x-1}{\sqrt{x}+2}+\dfrac{\sqrt{x}+6}{4-x}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-1\right)\)
\(=\dfrac{x\left(\sqrt{x}+2\right)-\left(x-1\right)\left(\sqrt{x}-2\right)-\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\dfrac{\sqrt{x}+2-\sqrt[]{x}+2}{\sqrt{x}-2}\)
\(=\dfrac{x\sqrt{x}+2x-x\sqrt{x}+2x+\sqrt{x}-2-\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{4}\)
\(=\dfrac{4x-8}{4\left(\sqrt{x}+2\right)}=\dfrac{x-2}{\sqrt{x}+2}\)
3:
\(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{x-2\sqrt{x}+1}\)
\(=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
4: \(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}+\dfrac{a}{b-a}\right):\left(\dfrac{a}{\sqrt{a}+\sqrt{b}}-\dfrac{a\sqrt{a}}{a+b+2\sqrt{ab}}\right)\)
\(=\dfrac{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-a}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}:\dfrac{a\left(\sqrt{a}+\sqrt{b}\right)-a\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)^2}\)
\(=\dfrac{-\sqrt{ab}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}:\dfrac{a\sqrt{a}+a\sqrt{b}-a\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)^2}\)
\(=-\dfrac{\sqrt{ab}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\cdot\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{a\sqrt{b}}\)
\(=\dfrac{-\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}\)
5: \(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}+2}-\dfrac{\sqrt{a}}{\sqrt{a}-2}+\dfrac{4\sqrt{a}-1}{a-4}\right):\dfrac{1}{\sqrt{a}+2}\)
\(=\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)-\sqrt{a}\left(\sqrt{a}+2\right)+4\sqrt{a}-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\dfrac{\sqrt{a}+2}{1}\)
\(=\dfrac{a-2\sqrt{a}-a-2\sqrt{a}+4\sqrt{a}-1}{\sqrt{a}-2}\)
\(=\dfrac{-1}{\sqrt{a}-2}\)
6: \(P=\left(1-\dfrac{2}{2-\sqrt{x}}\right):\left(\dfrac{\sqrt{x}-2}{x-\sqrt{x}-2}+\dfrac{x}{x+\sqrt{x}}\right)\)
\(=\left(1+\dfrac{2}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}+1\right)}+\sqrt{x}\cdot\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\sqrt{x}-2+2}{\sqrt{x}-2}:\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}+1}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
`1,` $B = \left(\frac{15-\sqrt{x}}{x-25}+\frac{2}{\sqrt{x}+5}\right) : \frac{\sqrt{x}+1}{\sqrt{x}-5} + \frac{\sqrt{x}}{\sqrt{x}+1}$
$= \frac{15-\sqrt{x}+2(\sqrt{x}-5)}{(\sqrt{x}-5)(\sqrt{x}+5)} \cdot \frac{\sqrt{x}+1}{\sqrt{x}-5} + \frac{\sqrt{x}}{\sqrt{x}+1}$
$= \frac{15-\sqrt{x}+2\sqrt{x}-10}{(\sqrt{x}-5)(\sqrt{x}+5)} \cdot \frac{\sqrt{x}+1}{\sqrt{x}-5} + \frac{\sqrt{x}}{\sqrt{x}+1}$
$= \frac{1+\sqrt{x}}{\sqrt{x}+1} \cdot \frac{1}{\sqrt{x}-5} + \frac{\sqrt{x}}{\sqrt{x}+1}$
$= 1$
`2,` $A = \left(\frac{x}{x+2} - \frac{x-1}{x-2} + \frac{\sqrt{x}+6}{4-x}\right) : \left(\frac{\sqrt{x}+2}{\sqrt{x}-2} - \frac{1}{\sqrt{x}+2}\right)$
$= \frac{x(x-2)-(x-1)(x+2)+(\sqrt{x}+6)(2-\sqrt{x})}{(x+2)(x-2)} \frac{(\sqrt{x}+2)^2-(\sqrt{x}-2)}{(x-2)(\sqrt{x}+2)}$
$= \frac{x^2-2x-x^2-x+2+2\sqrt{x}-x-6}{(x+2)(x-2)} : \frac{x+4\sqrt{x}+4-x+2}{(x-2)(\sqrt{x}+2)}$
$= \frac{4x-8}{(x-2)(x+2)} \cdot \frac{(x-2)(\sqrt{x}+2)}{4\sqrt{x}+6}$
$= \frac{4(\sqrt{x}+2)}{\sqrt{x}+2}$

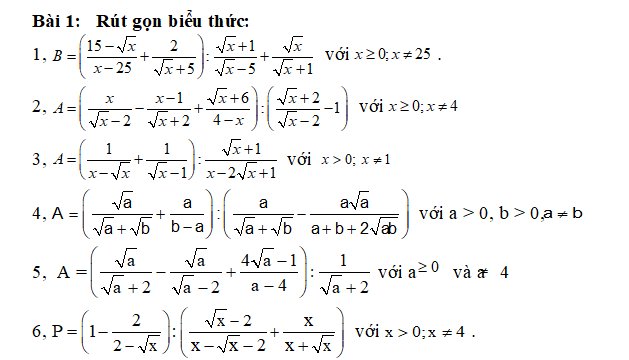






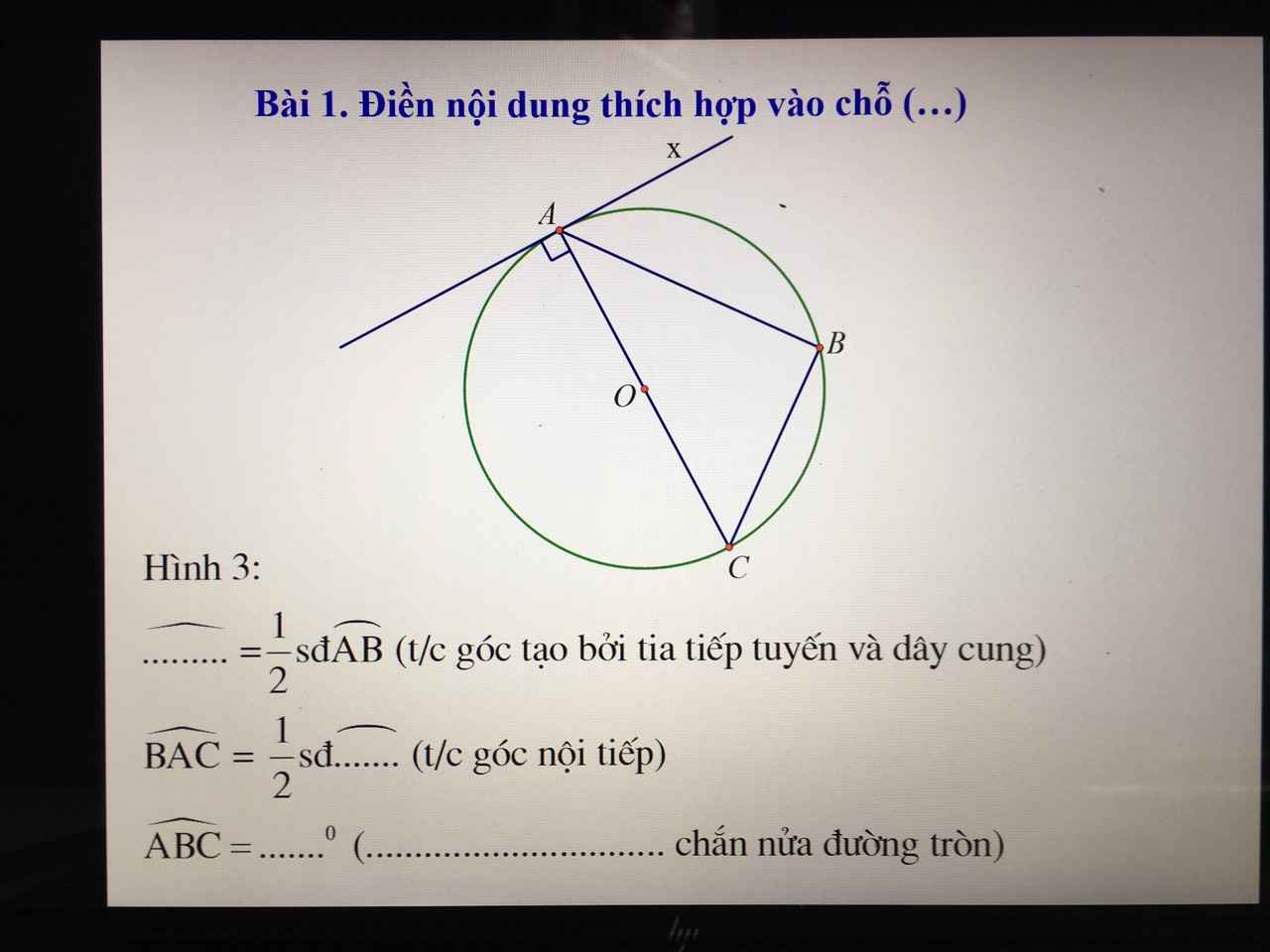



 Cho 3 số dương a,b,c thỏa mãn a+b+c=1. CMR:
Cho 3 số dương a,b,c thỏa mãn a+b+c=1. CMR: