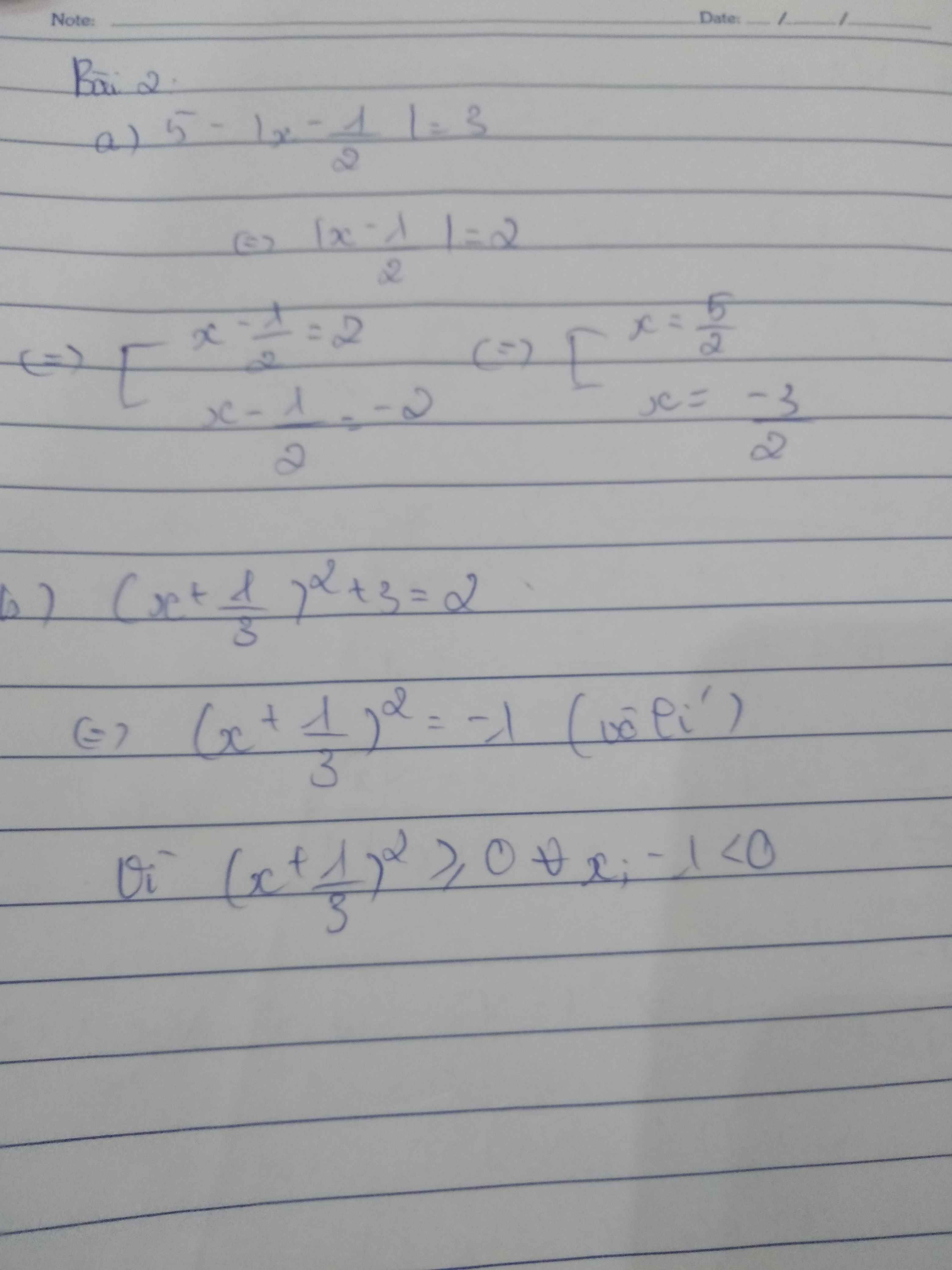Vì BC và Cx là 2 tia đối nên \(\widehat{BCA}\) và \(\widehat{ACx}\) là 2 góc kề bù
\(\Rightarrow\widehat{ACB}+\widehat{ACx}=180^o\)
\(40^o+\widehat{ACx}=180^o\)
\(\widehat{ACx}=140^o\)
b) Ta có:\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng 3 góc trong 1 tam giác)
\(40^o+\widehat{ABC}+70^o=180^o\)
\(\widehat{ABC}=70^o\)(1)
Vì Oy là phân giác của \(\widehat{ACx}\) nên \(\widehat{xCy}=\dfrac{\widehat{ACx}}{2}=\dfrac{140^o}{2}=70^o\)(2)
Từ (1),(2) => \(\widehat{ABC}=\widehat{xCy}\)
c)Cặp góc đồng vị là \(\widehat{ABC}\) và \(\widehat{xCy}\)
\(5-\left|x-\dfrac{1}{2}\right|=3\)
\(\left|x-\dfrac{1}{2}\right|=5-3\)
\(\left|x-\dfrac{1}{2}\right|=2\)
=>\(x-\dfrac{1}{2}=2\) hoặc \(x-\dfrac{1}{2}=-2\)
\(x=2+\dfrac{1}{2}\) \(x=-2+\dfrac{1}{2}\)
\(x=\dfrac{5}{2}\) \(x=\dfrac{-3}{2}\)
Vậy...\(\left(x+\dfrac{1}{3}\right)^2+3=2\)
\(\left(x+\dfrac{1}{3}\right)^2=2-3\)
\(\left(x+\dfrac{1}{3}\right)^2=-1\)
Vi \(\left(x+\dfrac{1}{3}\right)^2\) luôn luôn lớn hơn 0 nên
\(\left(x+\dfrac{1}{3}\right)^2=-1\)(vô lý)
Bài 2:
a) Ta có: \(5-\left|x-\dfrac{1}{2}\right|=3\)
\(\Leftrightarrow\left|x-\dfrac{1}{2}\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=2\\x-\dfrac{1}{2}=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-3}{2}\end{matrix}\right.\)
Bài 2:
b) Ta có: \(\left(x+\dfrac{1}{3}\right)^2+3=2\)
\(\Leftrightarrow\left(x+\dfrac{1}{3}\right)^2=-1\)(Vô lý)