a) ĐK: \(x>1\)
b) \(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}\)
\(=\dfrac{x+\sqrt{x}}{x-1}=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(x=\dfrac{9}{4}\) thay vào A, ta có:
\(A=\dfrac{\sqrt{\dfrac{9}{4}}}{\sqrt{\dfrac{9}{4}}-1}=\dfrac{\dfrac{3}{2}}{\dfrac{3}{2}-1}=3\)
c) để A<1
\(\Rightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}< 1\)
\(\Rightarrow\sqrt{x}< \sqrt{x}-1\)
\(\Rightarrow0< -1\left(\text{vô lí}\right)\)
⇒ A>1
a) ĐK: \(x>1\)
b) \(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}\)
\(=\dfrac{x+\sqrt{x}}{x-1}=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(x=\dfrac{9}{4}\) thay vào A, ta có:
\(A=\dfrac{\sqrt{\dfrac{9}{4}}}{\sqrt{\dfrac{9}{4}}-1}=\dfrac{\dfrac{3}{2}}{\dfrac{3}{2}-1}=3\)
c) để A<1
\(\Rightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}< 1\)
\(\Rightarrow\sqrt{x}< \sqrt{x}-1\)
\(\Rightarrow0< -1\left(\text{vô lí}\right)\)
⇒ A>1
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn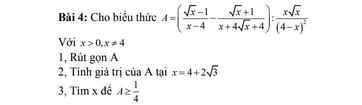
Mn giúp e với