câu 6:
a,áp dụng pytago\(=>BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10cm\)
do \(\Delta ABC\) vuông tại A có AM là trung tuyến
\(=>AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5cm\)
b, xét \(\Delta ABC\) và \(\Delta HBA\) có: \(\angle\left(B\right)\) chung
\(\angle\left(A\right)=\angle\left(AHB\right)=90^o\)\(=>\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(=>\dfrac{AB}{HB}=\dfrac{BC}{AB}=>AB^2=HB.BC\)
c, điểm K trong đề bài không có bạn ơi.
Câu 8:
a, \(xét\) \(\Delta ABH\) và \(\Delta CBA\) có: \(\angle\left(B\right)chung\)
\(\angle\left(A\right)=\angle\left(AHB\right)=90^0\)\(=>\Delta ABH\sim\Delta CBA\left(g.g\right)\)
\(=>\dfrac{AB}{BC}=\dfrac{BH}{AB}< =>AB^2=BH.BC\)
b,\(\) có \(\angle\left(B\right)+\angle\left(C\right)=90^o\)
mà \(\angle\left(C\right)+\angle\left(HAC\right)=90^o=>\angle\left(HAC\right)=\angle\left(B\right)\)
mà \(\angle\left(AHB\right)=\angle\left(AHC\right)=90^o\)
\(=>\Delta AHB\sim\Delta CHA\left(g.g\right)\)
\(=>\dfrac{AH}{CH}=\dfrac{HB}{AH}=>AH^2=HB.CH\)
c, ta có \(BD\) là phân giác\(=>\angle\left(ABD\right)=\angle\left(HBI\right)\)
mà \(\angle\left(A\right)=\angle\left(IHB\right)=90^0=>\Delta ABD\sim\Delta HBI\left(g.g\right)\)
\(=>\dfrac{AB}{HB}=\dfrac{AD}{HI}=>AB.HI=AD.HB\)(dpcm)(1)
d,đề cứ sao sao ấy:D








 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn


 mn giải giúp em vơi ạ em đang cần gấp cảm ơn
mn giải giúp em vơi ạ em đang cần gấp cảm ơn

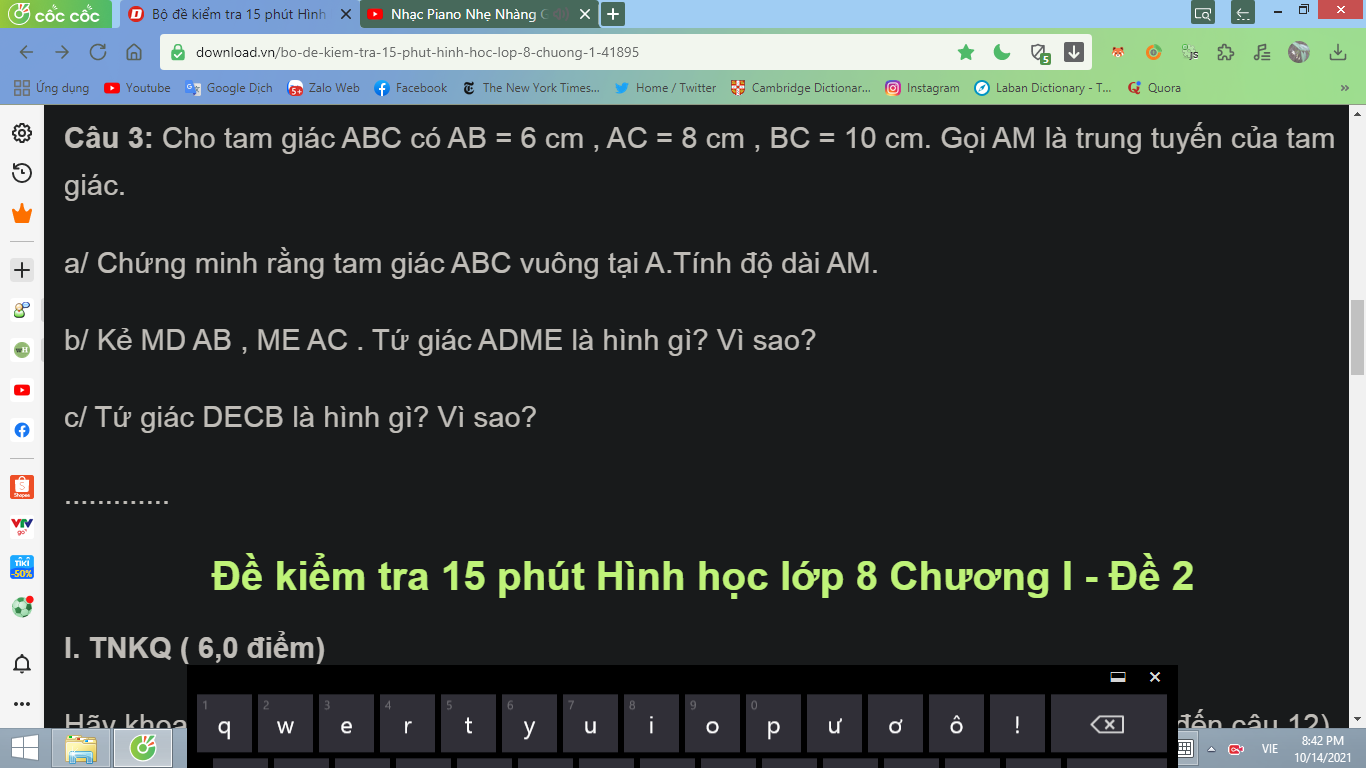





 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(