11c.
\(\left\{{}\begin{matrix}S_1^2=AD^2\\S_2^2=BD^2\end{matrix}\right.\) \(\Rightarrow\sqrt{S_1S_2}=AD.BD\) nên ta cần chứng minh: \(CD^2\le AD.BD\)
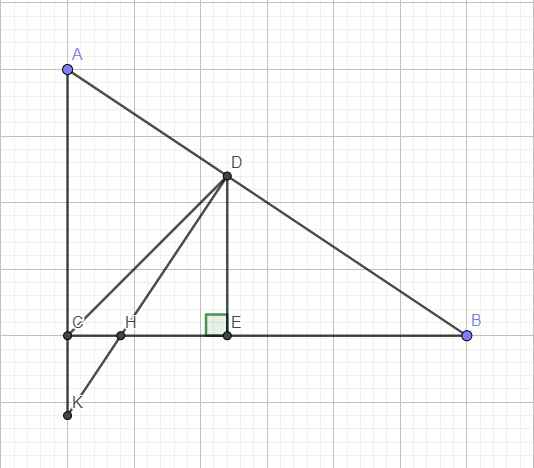
Kẻ \(DE\perp BC\Rightarrow\Delta CDE\) vuông cân tại E \(\Rightarrow CD^2=2DE^2\)
Mặt khác theo talet: \(\dfrac{DE}{AC}=\dfrac{BD}{AB}\Rightarrow DE=\dfrac{AC}{AB}.BD\Rightarrow2DE^2=2\dfrac{AC^2}{AB^2}.BD^2\)
Nên ta cần chứng minh: \(\dfrac{2AC^2}{AB^2}.BD^2\le AD.BD\Leftrightarrow\dfrac{2AC^2}{AB^2}\le\dfrac{AD}{BD}=\dfrac{AC}{BC}\)
\(\Leftrightarrow2AC.BC\le AB^2\)
Điều này đúng do: \(2AC.BC\le AC^2+BC^2=AB^2\) (đpcm)
Dấu "=" xảy ra khi D là trung điểm AB hay tam giác vuông cân tại C
12.
Ta có:
\(2=3\sqrt{xy}+2\sqrt{zx}\le\dfrac{3}{2}\left(x+y\right)+z+x\)
\(\Rightarrow5x+3y+2z\ge4\)
Mặt khác:
\(P=\dfrac{5yz}{x}+\dfrac{7zx}{y}+\dfrac{8xy}{z}=5\left(\dfrac{xy}{z}+\dfrac{zx}{y}\right)+3\left(\dfrac{yz}{x}+\dfrac{xy}{z}\right)+2\left(\dfrac{yz}{x}+\dfrac{zx}{y}\right)\)
\(P\ge5.2\sqrt{\dfrac{x^2yz}{yz}}+3.2\sqrt{\dfrac{xy^2z}{xz}}+2.2\sqrt{\dfrac{xyz^2}{xy}}=2\left(5x+3y+2z\right)\ge2.4=8\)
\(P_{min}=8\) khi \(x=y=z=\dfrac{2}{5}\)













 Nhờ mn giúp mình câu 1c và câu 2 ạ. Thanks
Nhờ mn giúp mình câu 1c và câu 2 ạ. Thanks

