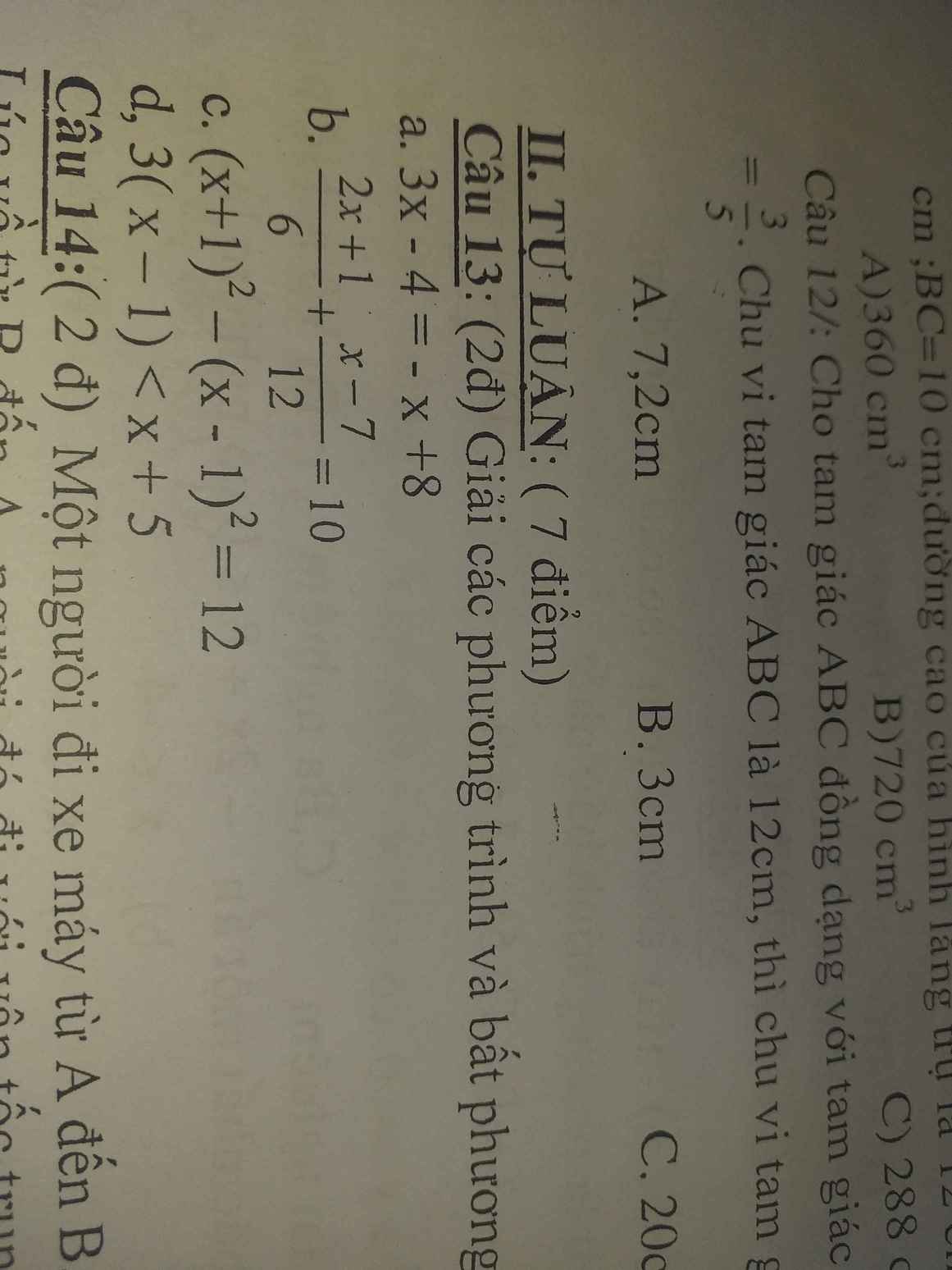\(A=\left(\dfrac{x+2}{x-2}+\dfrac{x-2}{x+2}\right).\dfrac{x^2-4}{x^2+4}\)
\(A=\left[\dfrac{\left(x+2\right)^2+\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\right].\dfrac{x^2-4}{x^2+4}\)
\(A=\dfrac{x^2+4x+4+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}.\dfrac{x^2-4}{x^2+4}\)
\(A=\dfrac{2\left(x^2+4\right)}{x^2-4}.\dfrac{x^2-4}{x^2+4}\)
`A=2`
\(=\dfrac{x^2+4x+4+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{x^2+4}\)
\(=\dfrac{2x^2+8}{x^2+4}=2\)








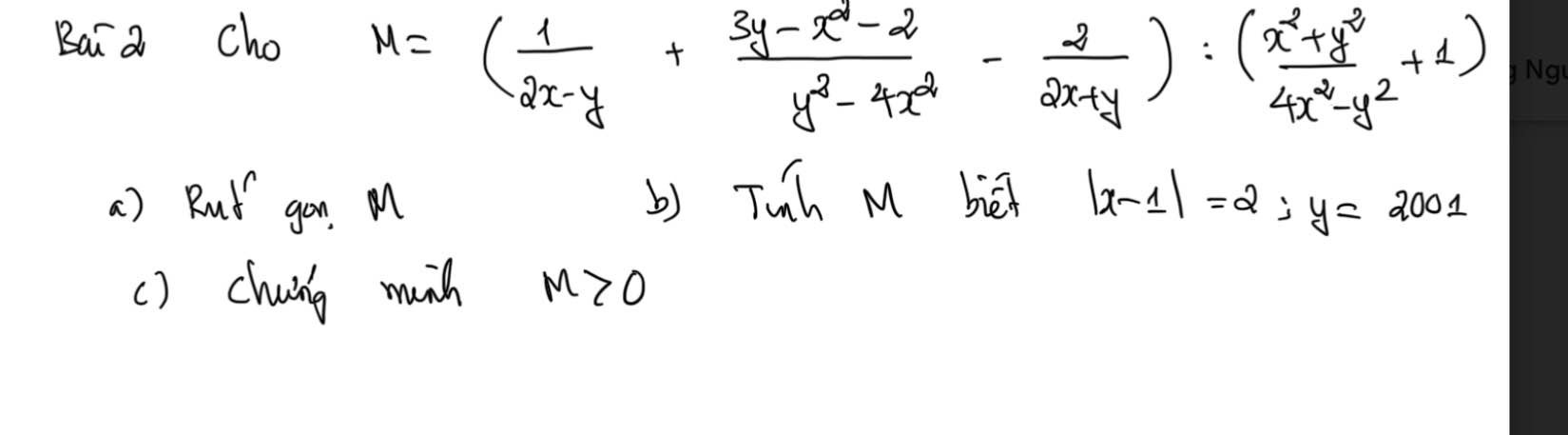







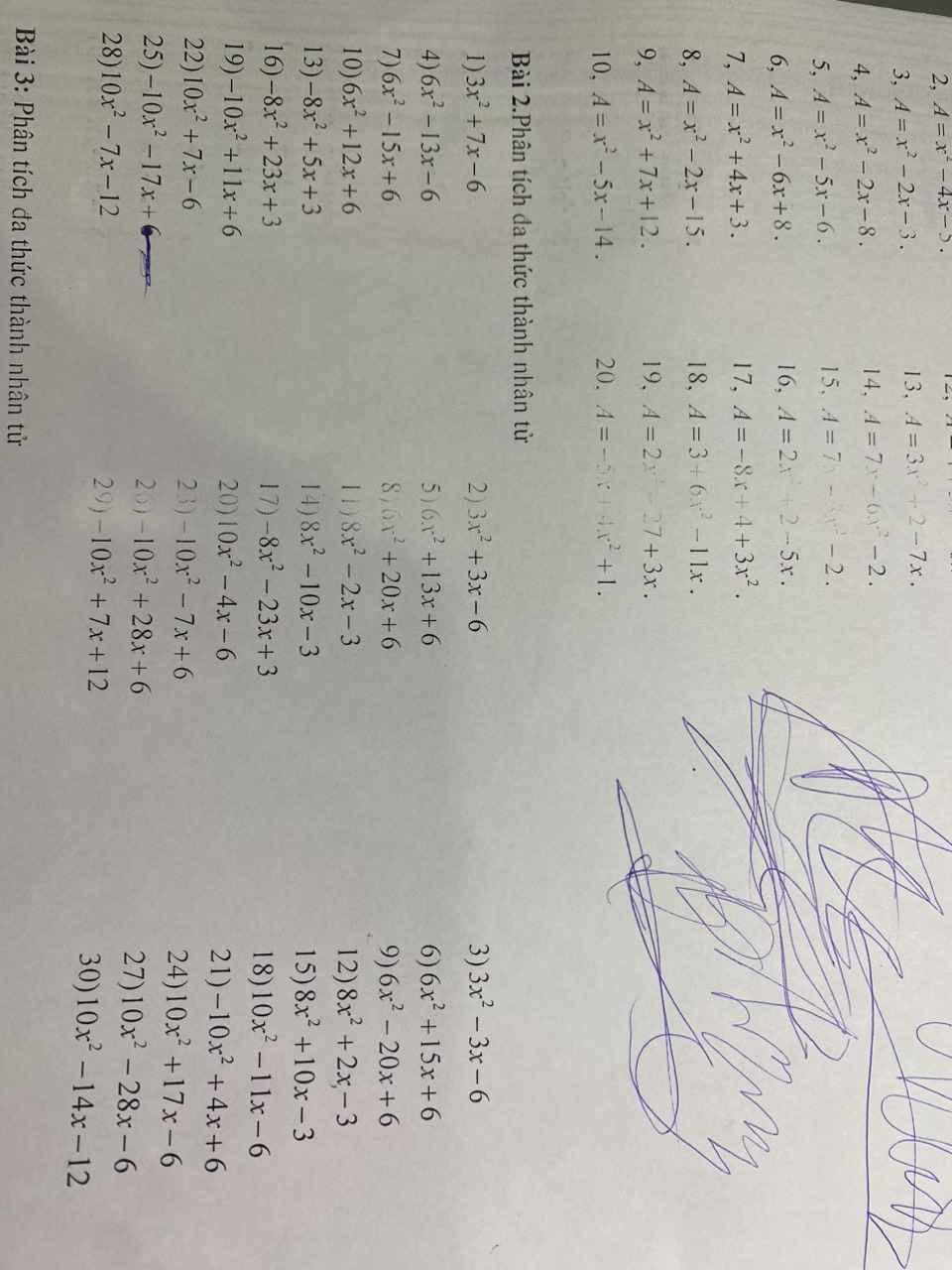



 Giup mình vs mình đg cần gấp cảm ơn mn trước ạ
Giup mình vs mình đg cần gấp cảm ơn mn trước ạ