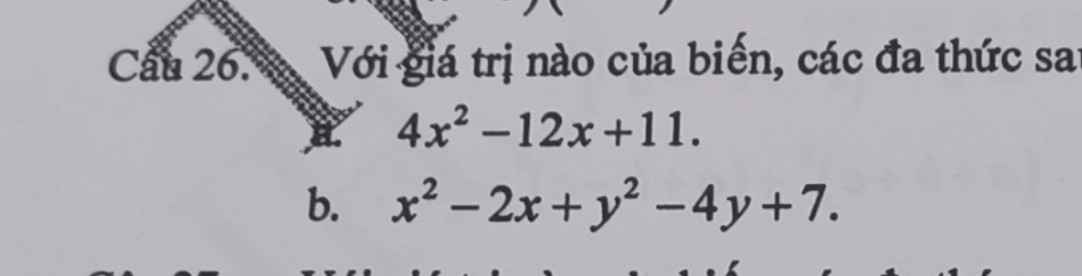Đề bài: Với giá trị nào của biến, các đa thức sau nhỏ nhất:
a) \(A\left(x\right)=4x^2-12x+11\)
Ta có: \(A\left(x\right)=4x^2-12x+11=\left(2x\right)^2-2.2x.3+9+2=\left(2x-3\right)^2+2\ge2\)
Dấu = xảy ra \(\Leftrightarrow\left(2x-3\right)^2=0\Leftrightarrow2x-3=0\Leftrightarrow x=\dfrac{3}{2}\)
b) \(B\left(x\right)=x^2-2x+y^2-4y+7\)
Ta có: \(B\left(x\right)=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
Dấu = xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\\left(y-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)