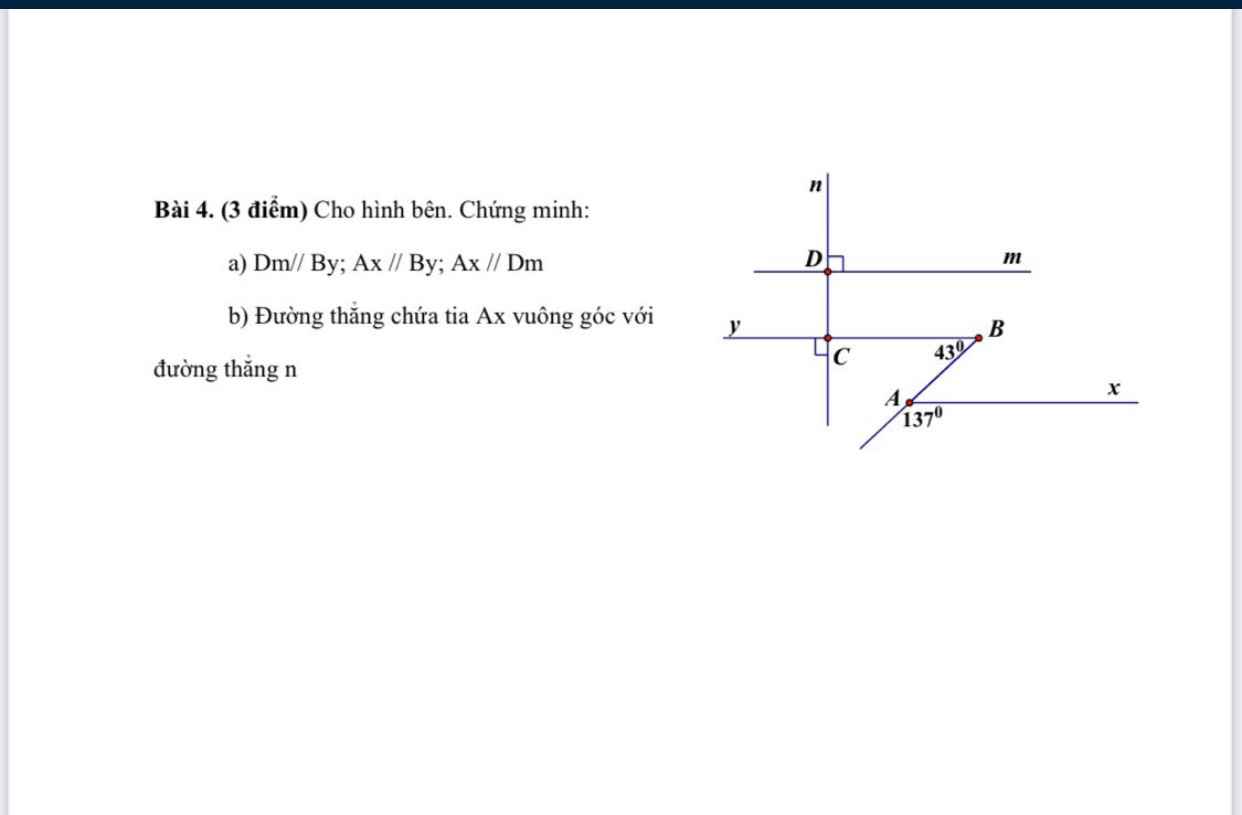
b: Ta có: \(\dfrac{3x-1}{2}=\dfrac{2x-2}{3}\)
\(\Leftrightarrow9x-3=4x-4\)
\(\Leftrightarrow x=-\dfrac{1}{5}\)
\(a,\Leftrightarrow\dfrac{2}{3}\left(3x-2\right)+\dfrac{4}{9}\left(3x-5\right)=-2x+1\\ \Leftrightarrow2x-\dfrac{4}{3}+\dfrac{4}{3}x-\dfrac{20}{9}+2x-1=0\\ \Leftrightarrow\dfrac{16}{3}x=\dfrac{41}{9}\Leftrightarrow x=\dfrac{41}{9}\cdot\dfrac{3}{16}=\dfrac{41}{48}\\ b,\Leftrightarrow3\left(3x-1\right)=2\left(2x-2\right)\\ \Leftrightarrow9x-3=4x-4\\ \Leftrightarrow5x=-1\Leftrightarrow x=-\dfrac{1}{5}\\ c,\Leftrightarrow15-2\left(x^2+1\right)=7\\ \Leftrightarrow13-2x^2=7\Leftrightarrow x^2=3\Leftrightarrow x=\pm\sqrt{3}\)
\(d,\Leftrightarrow x+1=\sqrt{x+1}\left(x\ge-1\right)\\ \Leftrightarrow x^2+2x+1=x+1\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)







 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU

 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!
 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy