2^3+x=32
2^3+x=2^4
Ta có:
3+x=4
X=4-3
X=1
`#3107.101107`
c)
`2^(x + 3) = 32`
`=> 2^(x + 3) = 2^5`
`=> x + 3 = 5`
`=> x = 5 - 3`
`=> x = 2`
Vậy, `x = 2`
d)
`20 - 2(x - 1)^2 = 2`
`=> 2(x - 1)^2 = 20 - 2`
`=> 2(x - 1)^2 = 18`
`=> (x - 1)^2 = 18 \div 2`
`=> (x - 1)^2 = 9`
`=> (x - 1)^2 = (+-3)^2`
`=>`\(\left[{}\begin{matrix}x-1=3\\x-1=-3\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
Vậy, `x \in {-2; 4}.`
____
b)
`(2x) \in` Ư`(20)` và `x > 8`
Ta có:
Ư`(20) = {1; 2; 3; 4; 5; 10; 20}`
`=> 2x \in {1; 2; 3; 4; 5; 10; 20}`
`=> x \in {1/2; 1; 3/2; 2; 5/2; 5; 10}`
Mà `x > 8`
`=> x = 10`
Vậy, `x = 10`
c)
`30 \vdots (x + 2)` và `x \le 15`
Ta có:
Ư`(30) = {1; 2; 3; 5; 6; 10; 15; 30}`
`=> (x + 2) \in {1; 2; 3; 5; 6; 10; 15; 30}`
`=> x \in {-1; 0; 1; 3; 4; 8; 13; 28}`
Mà `x \le 15 => x \in {-1; 0; 1; 3; 4; 8}`
Vậy, `x \in {-1; 0; 1; 3; 4; 8}.`

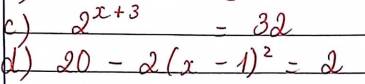
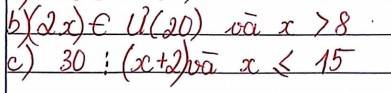















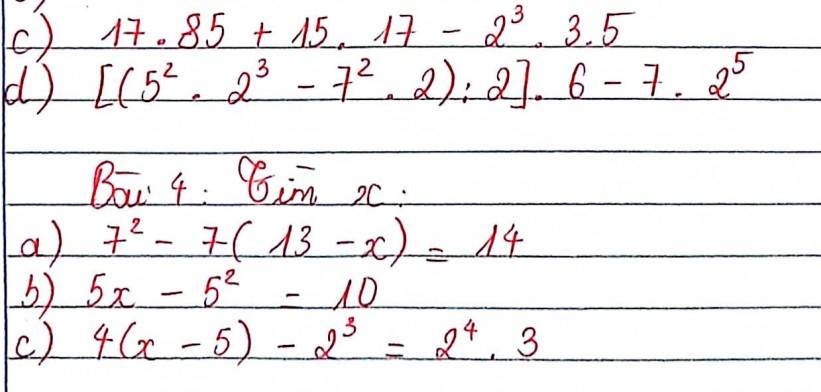

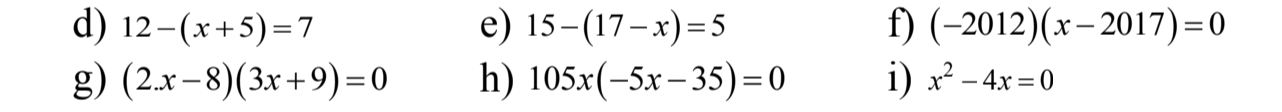



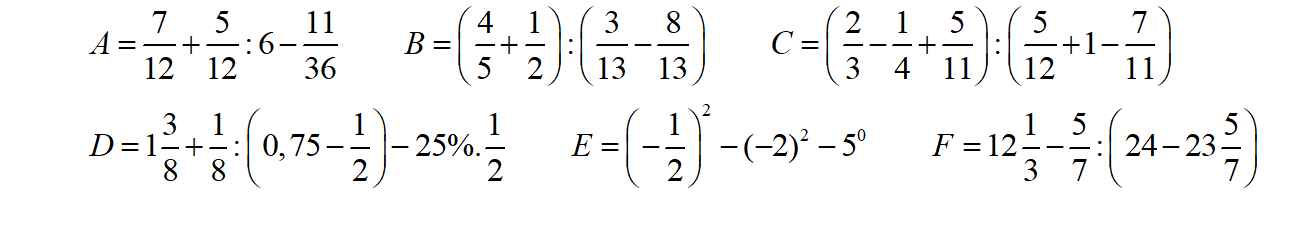

 Các Bạn Gíup mình vs ạ, mình đang cần khá gấp, cảm ơn ạ
Các Bạn Gíup mình vs ạ, mình đang cần khá gấp, cảm ơn ạ