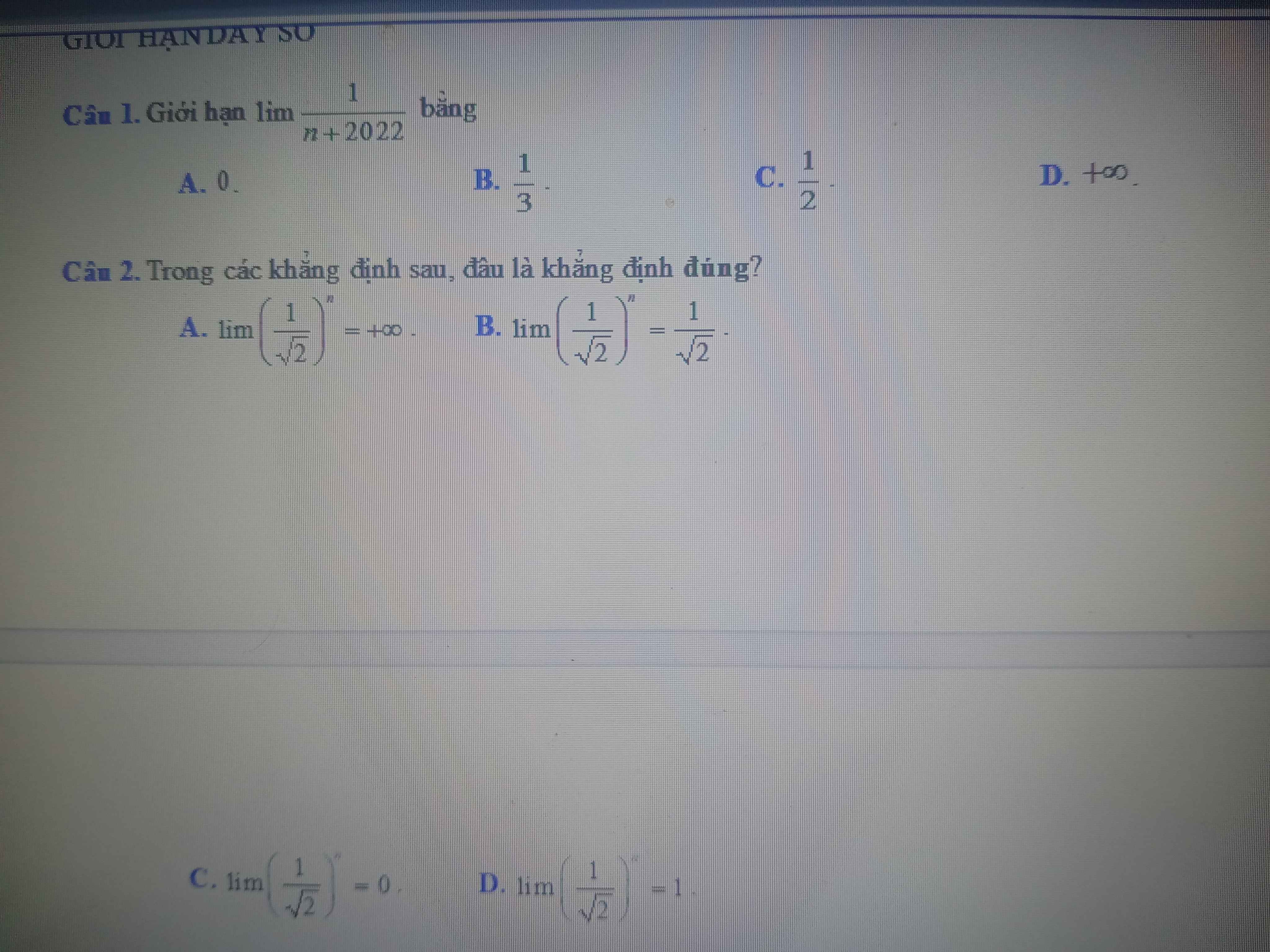
a: -1<=sinx<=1
=>-1-2<=sinx-2<=1-2
=>-3<=y<=-1
\(y_{min}=-3\) khi sin x=-1
=>\(x=-\dfrac{\Omega}{2}+k2\Omega\)
\(y_{max}=-1\) khi sinx=1
=>\(x=\dfrac{\Omega}{2}+k2\Omega\)
b: \(y=sinx+cosx=\sqrt{2}\cdot sin\left(x+\dfrac{\Omega}{4}\right)\)
\(-1< =sin\left(x+\dfrac{\Omega}{4}\right)< =1\)
=>\(-\sqrt{2}< =\sqrt{2}\cdot sin\left(x+\dfrac{\Omega}{4}\right)< =\sqrt{2}\)
=>\(-\sqrt{2}< =y< =\sqrt{2}\)
\(y_{min}=-\sqrt{2}\) khi \(sin\left(x+\dfrac{\Omega}{4}\right)=-1\)
=>\(x+\dfrac{\Omega}{4}=-\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=-\dfrac{3}{4}\Omega+k2\Omega\)
\(y_{max}=\sqrt{2}\) khi \(sin\left(x+\dfrac{\Omega}{4}\right)=1\)
=>\(x+\dfrac{\Omega}{4}=\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=\dfrac{\Omega}{4}+k2\Omega\)
c: \(y=4\cdot sinx-3\cdot cosx-5\)
\(=5\left(\dfrac{4}{5}\cdot sinx-\dfrac{3}{5}\cdot cosx\right)-5\)
\(=5\cdot\left(sinx\cdot cos\alpha-cosx\cdot sin\alpha\right)-5\)(Với \(cos\alpha=\dfrac{4}{5};sin\alpha=\dfrac{3}{5}\))
\(=5\cdot sin\left(x-\alpha\right)-5\)
\(-1< =sin\left(x-\alpha\right)< =1\)
=>\(-5< =5\cdot sin\left(x-\alpha\right)< =5\)
=>\(-10< =5\cdot sin\left(x-\alpha\right)-5< =0\)
=>-10<=y<=0
\(y_{min}=-10\) khi \(sin\left(x-\alpha\right)=-1\)
=>\(x-\alpha=-\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=-\dfrac{\Omega}{2}+k2\Omega+\alpha\)
\(y_{max}=0\) khi \(sin\left(x-\alpha\right)=1\)
=>\(x-\alpha=\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=\alpha+\dfrac{\Omega}{2}+k2\Omega\)
g: \(y=cos5x+cos\left(5x-\dfrac{\Omega}{3}\right)\)
\(=cos5x+cos5x\cdot cos\left(\dfrac{\Omega}{3}\right)+sin5x\cdot sin\left(\dfrac{\Omega}{3}\right)\)
\(=\dfrac{3}{2}\cdot cos5x+\dfrac{\sqrt{3}}{2}\cdot sin5x\)
\(=\sqrt{3}\left(\dfrac{\sqrt{3}}{2}\cdot cos5x+\dfrac{1}{2}\cdot sin5x\right)\)
\(=\sqrt{3}\cdot sin\left(5x+\dfrac{\Omega}{3}\right)\)
\(-\sqrt{3}< =\sqrt{3}\cdot sin\left(5x+\dfrac{\Omega}{3}\right)< =\sqrt{3}\)
=>\(-\sqrt{3}< =y< =\sqrt{3}\)
\(y_{min}=-\sqrt{3}\) khi \(sin\left(5x+\dfrac{\Omega}{3}\right)=-1\)
=>\(5x+\dfrac{\Omega}{3}=-\dfrac{\Omega}{2}+k2\Omega\)
=>\(5x=-\dfrac{5}{6}\Omega+k2\Omega\)
=>\(x=-\dfrac{\Omega}{6}+\dfrac{k2\Omega}{5}\)
\(y_{max}=\sqrt{3}\) khi \(sin\left(5x+\dfrac{\Omega}{3}\right)=1\)
=>\(5x+\dfrac{\Omega}{3}=\dfrac{\Omega}{2}+k2\Omega\)
=>\(5x=\dfrac{\Omega}{6}+k2\Omega\)
=>\(x=\dfrac{\Omega}{30}+\dfrac{k2\Omega}{5}\)
f: \(y=cos^4x-sin^4x\)
\(=\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)\)
\(=cos^2x-sin^2x=cos2x\)
Vì -1<=cos2x<=1
nên -1<=y<=1
\(y_{min}=-1\) khi cos2x=-1
=>\(2x=\Omega+k2\Omega\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
\(y_{max}=1\) khi cos2x=1
=>\(2x=k2\Omega\)
=>\(x=k\Omega\)