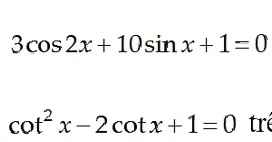a.
\(90^0< a< 180^0\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{2\sqrt{2}}{3}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{\sqrt{2}}{4}\)
b.
\(0< a< 90^0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
c.
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{3cosa}{sina}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{sin^2a+3cos^2a}{sin^2a+cos^2a}=1+2cos^2a=\dfrac{17}{8}\)
d.
\(A=\dfrac{\dfrac{cosa}{sina}+\dfrac{3sina}{cosa}}{\dfrac{2cosa}{sina}+\dfrac{sina}{cosa}}=\dfrac{cos^2a+3sin^2a}{2cos^2a+sin^2a}=\dfrac{cos^2a+3\left(1-cos^2a\right)}{2cos^2a+\left(1-cos^2a\right)}\)
\(=\dfrac{3-2cos^2a}{1+cos^2a}=\dfrac{19}{13}\)
e.
\(B=\dfrac{\dfrac{3cosa}{sina}+\dfrac{2sina}{cosa}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{3cos^2a+2sin^2a}{sin^2a+cos^2a}=3\left(1-sin^2a\right)+2sin^2a\)
\(=3-sin^2a=\dfrac{26}{9}\)
f.
\(C=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}=\dfrac{2tana+3}{tana+1}=\dfrac{7}{3}\)
g.
\(C=\dfrac{\dfrac{3sina}{sina}-\dfrac{4cosa}{sina}}{\dfrac{cosa}{sina}-\dfrac{2sina}{sina}}=\dfrac{3-4cota}{cota-2}=1+\sqrt{5}\)
h.
\(B=\dfrac{\dfrac{sina}{cosa}.\dfrac{1}{cos^2a}-\dfrac{cosa}{cosa}.\dfrac{1}{cos^2a}}{\dfrac{sin^3a}{cos^3a}+\dfrac{3cos^3a}{cos^3a}+\dfrac{2sina}{cosa}.\dfrac{1}{cos^2a}}=\dfrac{tana\left(1+tan^2a\right)-\left(1+tan^2a\right)}{tan^3a+3+2tana\left(1+tan^2a\right)}\)
\(=\) ... (bạn tự thay số \(tana=\sqrt{2}\) rồi tính toán)
i.
\(B=\dfrac{\dfrac{sina}{cosa}.\dfrac{1}{cos^2a}+\dfrac{2cosa}{cosa}.\dfrac{1}{cos^2a}}{\dfrac{sin^3a}{cos^3a}+\dfrac{2cos^3a}{cos^3a}-\dfrac{3sina}{cosa}.\dfrac{1}{cos^2a}}=\dfrac{tana\left(1+tan^2a\right)+2\left(1+tan^2a\right)}{tan^3a+2-3tana\left(1+tan^2a\right)}\)
\(=...\) (bạn tự thay số)