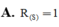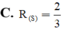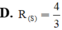Các câu hỏi tương tự
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 0, (Q): 2x - y - 2z + 1 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu? A. 4π B. π C. 2π D. 16π
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 = 0, (Q): 2x - y - 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?
A. 4π
B. π
C. 2π
D. 16π
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-20 và mặt phẳng (Q): 2x-y-2z+100 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó A.
r
4
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-2=0 và mặt phẳng (Q): 2x-y-2z+10=0 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
A. r = 4 2 3
B. r = 2 2 3
C. r = 5 3
D. r = 2 5 3
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng
(
Q
)
:
x
+
2
y
–
2
z
+
1
0
và tiếp xúc với mặt cầu
(
S
)
:
x
2
+
y
2...
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y – 2 z + 1 = 0 và tiếp xúc với mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x – 4 y – 2 z – 3 = 0
A. x + 2 y – 2 z + 6 = 0 ; x + 2 y – 2 z – 12 = 0
B. x + 2 y – 2 z + 8 = 0 ; x + 2 y – 2 z – 10 = 0
C. x + 2 y – 2 z + 10 = 0 ; x + 2 y – 2 z – 8 = 0 .
D. x + 2 y – 2 z + 12 = 0 ; x + 2 y – 2 z – 6 = 0
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng
(
Q
)
:
x
+
2
y
-
2
z
+
1
0
và tiếp xúc với mặt cầu
(
S
)
:
x
2
+
y
2
+...
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng ( Q ) : x + 2 y - 2 z + 1 = 0 và tiếp xúc với mặt cầu ( S ) : x 2 + y 2 + z 2 + 2 x – 4 y – 2 z – 3 = 0
A. x + 2 y – 2 z + 12 = 0 v à x + 2 y – 2 z - 6 = 0
B. x + 2 y – 2 z – 12 = 0 v à x + 2 y – 2 z + 6 = 0
C. x + 2 y – 2 z + 10 = 0 v à x + 2 y – 2 z - 8 = 0
D. x + 2 y – 2 z – 10 = 0 v à x + 2 y – 2 z + 8 = 0
Trong không gian Oxyz, cho mặt cầu (S) tâm O(0;0;0) và tiếp xúc với mặt phẳng(α): 2x+y+2z-60. Tính bán kính của (S). A. 1 B. 3 C. 2 D. 6.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) tâm O(0;0;0) và tiếp xúc với mặt phẳng(α): 2x+y+2z-6=0. Tính bán kính của (S).
A. 1
B. 3
C. 2
D. 6.
Cho mặt cầu
S
:
x
2
+
y
2
+
z
2
9
và
P
2
x
-
y
+
2
z
-
9
0
. Gọi (Q) là mặt phẳng song song với (P) và (Q) tiếp xúc (S) tại M. Tìm tọa độ M.
Đọc tiếp
Cho mặt cầu S : x 2 + y 2 + z 2 = 9 và P 2 x - y + 2 z - 9 = 0 . Gọi (Q) là mặt phẳng song song với (P) và (Q) tiếp xúc (S) tại M. Tìm tọa độ M.
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm I(4;0;1) và mặt phẳng
P
:
2
x
-
y
+
2
z
-
1
0
. Phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P) là
Đọc tiếp
Trong không gian Oxyz, cho điểm I(4;0;1) và mặt phẳng P : 2 x - y + 2 z - 1 = 0 . Phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P) là
![]()
![]()
![]()
![]()
Trong không gian
O
x
y
z
cho mặt cầu
(
s
)
:
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
1...
Đọc tiếp
Trong không gian O x y z cho mặt cầu ( s ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 1 ) 2 = 6 tiếp xúc với hai mặt phẳng ( P ) : x + y + 2 z + 5 = 0 , ( Q ) : 2 x - y + z - 5 = 0 lần lượt tại A và B. Độ dài đoạn thẳng AB là
A. 2 6
B. 3
C. 3 2
D. 2 3
Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng
∆
:
x
-
3
2
y
-
1
-
1
z
-
1
2
đồng thời tiếp xúc với hai mặt phẳng (α1): 2x+2y+z-60 và (α2): x-2y+2z0 A. 1 B. 0. C. Vô số...
Đọc tiếp
Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng ∆ : x - 3 2 = y - 1 - 1 = z - 1 2 đồng thời tiếp xúc với hai mặt phẳng (α1): 2x+2y+z-6=0 và (α2): x-2y+2z=0
A. 1
B. 0.
C. Vô số
D. 2.